Silvia Joachim, Karl Haberl und Franz Embacher
|
Über diesen Lernpfad
Hier sollen sich die SchülerInnen mit der Variation von Parametern in Sinus- und Kosinusfunktionen beschäftigen und ihre Auswirkung erarbeiten und beschreiben können.
Kompetenzen
|
Das kannst du schon
- Darstellungsformen von Funktionen
- Kenntnis der Auswirkung von Variationen in den Darstellungsformen von linearen und quadratischen Funktionen
- Eigenschaften der trigonometrischen Funktionen
|
Das kannst du lernen
- Erkennen der Auswirkung der Variation von Parametern im Funktionsterm auf die Graphen der Sinus- und Kosinusfunktion und umgekehrt.
|
|
 |
Hallo! Wäre es nicht toll, wenn du hellsehen könntest? Wenn du den Graphen eines Funktionsterms auch ohne Wertetabelle direkt zeichnen könntest? Wenn du aus dem Graphen einer Funktion deren Term ablesen könntest?
Für die linearen und die quadratischen Funktionen beherrschst du diese Kunst wahrscheinlich schon. Dann wirst du vieles von deinem Wissen auf die allgemeine Sinus- und Kosinusfunktion übertragen können.
|
|
|
Hinweise:
- Denke bitte daran die Hefteinträge in dein Heft zu übernehmen!
- Bei den GeoGebra-Applets ist die
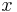 -Achse mit Vielfachen von -Achse mit Vielfachen von 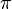 beschriftet. Indem man die beschriftet. Indem man die 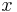 -Achse mit der rechten Maustaste anklickt und "Eigenschaften" wählt, kann man auf die Einheit cm umstellen. -Achse mit der rechten Maustaste anklickt und "Eigenschaften" wählt, kann man auf die Einheit cm umstellen.
- Zu den meisten Aufgaben gibt es Lösungen, diese befinden sich am Ende der jeweiligen Seite. Bearbeite zuerst die Aufgaben, mache dir Notizen und vergleiche diese erst zum Schluss mit den Lösungen!
|
|
|
Dieser Lernpfad besteht aus drei Stationen, die du am besten nacheinander bearbeitest. Klicke dazu einfach auf die gewünschte Station!
<graphviz>
digraph G {
rankdir=RL;
"Term" -> "Graph"[label=" "];
edge [color = white]; "Term" -> "Hellsehen";
"Hellsehen" -> "Graph";
edge [color = black]; rankdir=LR;
"Graph" -> "Term";
}
</graphviz>
|
-
|
Physik-Ecke
Experimentier-Ecke
Aufgabe 
Du hast doch bestimmt einen Zirkel, oder? Genauer gesagt benötigst du nicht den Zirkel, sondern nur die Bleistiftmine für dieses Experiment. Die Mine sollte schräg angefeilt sein. Nimm die Mine aus dem Zirkel und lege sie auf ein Blatt Papier. Wenn du die Mine nun mit einem leichten Druck über das Papier rollst, kannst du den Graphen einer Sinusfunktion erkennen. Diesen kannst du dann gerne noch mit einem Stift nachfahren.
|
|
|
|
zw:Trigonometrische Funktionen

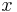 -Achse mit Vielfachen von
-Achse mit Vielfachen von 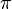 beschriftet. Indem man die
beschriftet. Indem man die 

