Zusatzaufgaben
Einführung - Station 1: Einfluss der Parameter - Station 2: Bestimmung der Funktionsgleichung und mehr - Station 3: Anwendungen in der Physik - Station 4: Zusatzaufgaben
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Experimentier-Ecke
|
Du hast doch bestimmt einen Zirkel, oder? Genauer gesagt benötigst du nicht den Zirkel, sondern nur die Bleistiftmine für dieses Experiment. Die Mine sollte schräg angefeilt sein. Nimm die Mine aus dem Zirkel und lege sie auf ein Blatt Papier. Wenn du die Mine nun mit einem leichten Druck über das Papier rollst, kannst du den Graphen einer Sinusfunktion erkennen. Diesen kannst du dann gerne noch mit einem Stift nachfahren. |
Zusatzaufgaben
|
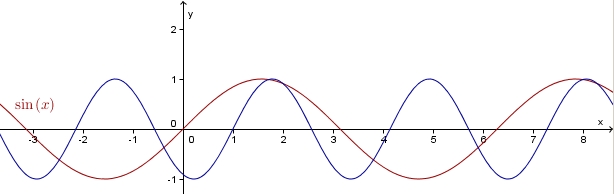
In dem unteren Bild sind die Sinuskurve (rot) und ein Graph einer allgemeinen Sinusfunktion (schwarz) zu sehen.
|
|
Lösung zu Aufgabe Z1:
Nullstellen der Sinusfunktion: 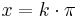 mit
mit  oder
oder 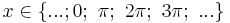
Nullstellen: 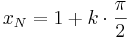 mit
mit  oder
oder 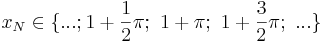
Hochpunkte: 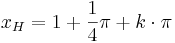 mit
mit  oder
oder 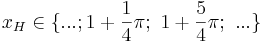
Tiefpunkte: 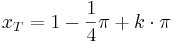 mit
mit  oder
oder 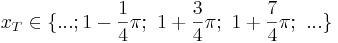
streng monoton fallend: ![...;\ [\frac{1}{12}\pi;\ \frac{7}{12}\pi];\ [\frac{13}{12}\pi;\ \frac{19}{12}\pi];\ ...](/images/math/2/3/5/2352ffad5112a215b1551af34791f362.png)
streng monoton steigend: ![...;\ [-\frac{5}{12}\pi;\ \frac{1}{12}\pi];\ [\frac{7}{12}\pi;\ \frac{13}{12}\pi];\ [\frac{19}{12}\pi;\ \frac{25}{12}\pi];\ ...](/images/math/a/b/3/ab3f03ffd65ea28a0ffd4a78e3cd5295.png)
a) Die Nullstellen der Sinusfunktion sind bei allen Vielfachen von PI, also x = k*PI.
b) Die Nullstellen der "schwarzen" Funktion sind bei x = 1, 1+PI/2, 1+PI, ...
c) Hochpunkte sind bei x = 1 + PI/4, 1 + 5/4*PI, ...
Tiefpunkte sind bei x = 1 - PI/4, 1 + 3/4*PI, ...
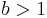 den Parameter
den Parameter  änderst?
änderst?
