Numerische Näherung - Heronverfahren

Numerische Näherung - Heronverfahren

Das Heron-Verfahren (auch babylonisches Wurzelziehen genannt) ist ein rekursives Näherungsverfahren zur Berechnung der Quadratwurzel einer Zahl, das von Heron von Alexandria erstmals beschreiben wurden.

Datei:Heron von Alexandria.jpg

Heron von Alexandria; Quelle: http://de.wikioedia.org

Die Iterationsvorschrift zur Berechnung der Wurzel aus 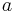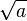$\,a$ ($\sqrt{a}$) lautet: $x_{n+1}=\frac{x_{n}+\frac{a}{x_{n}}}{2}$

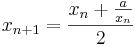
Der Startwert der Iteration kann dabei (ungleich Null!) beliebig positiv festgesetzt werden.

Derartige Rekursionen lassen sich mittels jeder Programmiersprache oder auch mit den Möglichkeiten eines Computer-Algebra-Systems (CAS) darstellen. Eine alternative Möglichkeit ist die Verwendung einer Tabellenkalkulation.

Lösungsansätze:

• CAS am Beispiel der Open-Source-Software MAXIMA (Download unter http://maxima.sourceforge.net): Lösung mit Maxima
• Tabellenkalkulation: Lösung mit Excel