Rekursive Beschreibung von Veränderungen
Unter rekursiven Verfahren kannst Du Dir Verfahren vorstellen, die errechnete Ergebnisse einer Formel wieder als Anfangswerte in die Formel einsetzen. Rekursion ist lateinisch und bedeutet zurücklaufen.
Rekursive Verfahren sind im Allgemeinen schrittweise (iterative) Verfahren. Das beudeutet, dass Du kein Ergebnis einfach ausrechnest, sonder Dich (langsam) an ein Ergebnis herantastest. Du näherst Dich Schritt für Schritt einem (richtigen) Ergebnis. Die Ergebnisse aus der Rekursionsformel sind die schrittweisen Zwischenergebnisse, die zum (korrekten) Endergebnis führen.
Da Differentialgleichungen schwierig zu lösen sind, ist es oft einfacher diese Art von Gleichungen in eine Differenzengleichung umzuwandeln und dann diese zu lösen. Differenzengleichungen sind rekursive Verfahren und können entsprechend gelöst werden.
Inhaltsverzeichnis |
Differenzengleichung
Begriffsbildung
Eine Differenzengleichung ist eine Möglichkeit, dynamische Systeme abzubilden. Dabei wird eine Folge von diskreten (einzeln betrachtbaren, abzählbaren) Ereignissen rekursiv definiert. Jedes Folgenglied ist daher eine Funktion der vorhergehenden Folgenglieder.
Form: 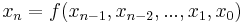 für natürliche Zahlen
für natürliche Zahlen 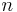 .
.
Die Veränderung wird durch den Differenzenquotienten angegeben:
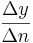 mit
mit 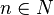
Dabei entspricht:
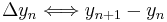 und damit beispielsweise
und damit beispielsweise 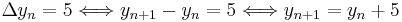
Weiterführende Links:
- Differenzengleichungen, Josef Leydold, Differenzengleichungen, Abt. f. angewandte Statistik und Datenverarbeitung der WU Wien, 1997
- Systemdynamik, Peter Zierler, Systemdynamik - Querverbindung zwischen Mathematik und Informatik, NOEBIS
Software zur dynamischen Modellierung:

