Startseite --- Die Wurzelfunktion - Übungen - Anwendungen - Weitere Eigenschaften --- Die allgemeine Wurzelfunktion - Übungen und Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
|
Bei den folgenden Aufgaben bearbeitest du den Zusammenhang zwischen dem Flächeninhalt eines Quadrats und seiner Seitenlänge.
Ein Quadrat mit Seitenlänge  hat den Flächeninhalt hat den Flächeninhalt 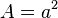 . .
Ist die Seitenlänge 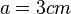 , dann ist also der Flächeninhalt , dann ist also der Flächeninhalt 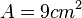 . .
Umgekehrt ist dann für ein Quadrat mit Flächeninhalt 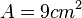 die zugehörige Seitenlänge die zugehörige Seitenlänge 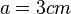 . .
Wie kannst du die Seitenlänge eines Quadrats bei gegebenem Flächeninhalt berechnen?
[Lösung anzeigen][Lösung ausblenden]
Aufgabe 2 
a) Setze in deine Formel verschiedene Werte für A ein und berechne a! Trage die Ergebnisse in eine Wertetabelle ein!
b) Stelle deine Wertepaare im Koordinatensystem (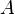 entspricht der x-Achse, entspricht der x-Achse,  entspricht der y-Achse) dar! entspricht der y-Achse) dar!
|
In der vorherigen Aufgabe hast du einigen Flächeninhalten exemplarisch ihre Seitenlänge zugeordnet. Mit dem folgenden Applet kannst du diesen Zusammenhang verallgemeinern.
 Merke
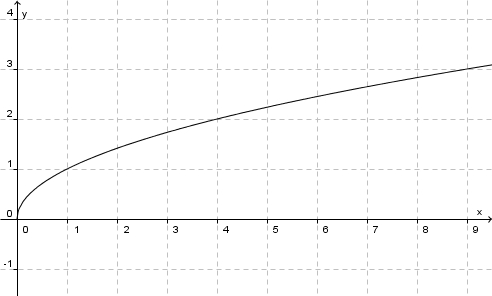
Die Funktion  , die jeder nicht negativen reellen Zahl x ihre Quadratwurzel , die jeder nicht negativen reellen Zahl x ihre Quadratwurzel 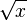 zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion. zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.
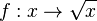
Ihr Graph schaut so aus:
|
Aufgabe 4 
Gib für die Quadratwurzelfunktion Definitions- und Wertemenge an.
|
Aufgabe 1
[Lösung anzeigen][Lösung ausblenden]
a) 1; 2,25; 4; 6,25; 9
b) A(a) = a2
c) 25; 100, 225
d) 1,2; 1,4; 1,5; 2,7
Aufgabe 2 [Lösung anzeigen][Lösung ausblenden]
Dein Ergebnis kann so aussehen.
a) 
b) 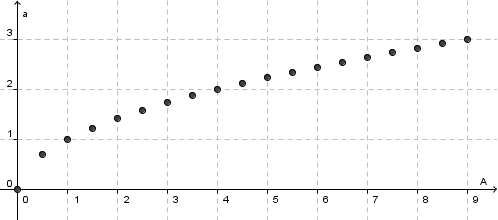
Aufgabe 3 [Lösung anzeigen][Lösung ausblenden]
Aufgabe 4 [Lösung anzeigen][Lösung ausblenden]
Die Wurzelfunktion hast du nun kennengelernt. Als nächstes kannst du zu Übungen oder Anwendungen oder Weitere Eigenschaften gehen.
|
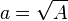
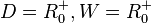
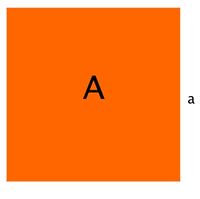
 hat den Flächeninhalt
hat den Flächeninhalt 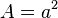 .
.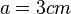 , dann ist also der Flächeninhalt
, dann ist also der Flächeninhalt 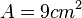 .
. 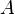 zugeordnet.
zugeordnet. 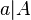 ). Mit dem Schieberegler kannst du verschiedene Werte für
). Mit dem Schieberegler kannst du verschiedene Werte für  , die jeder nicht negativen reellen Zahl x ihre Quadratwurzel
, die jeder nicht negativen reellen Zahl x ihre Quadratwurzel 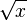 zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.
zuordnet heißt Quadratwurzelfunktion oder einfach nur Wurzelfunktion.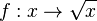


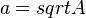 dar.
dar.

