Wurzelfunktionen didaktischer Kommentar

Zurück zur Startseite: Wurzelfunktionen

---

Didaktischer Kommentar

Dieser Lernpfad beschäftigt sich mit Wurzelfunktionen und zwar mit

• deren verschiedenen Darstellungsformen (Graph, Tabelle, Formel),
• den Eigenschaften von Wurzelfunktionen (Definitionsmenge, Wertemenge, mittlere Änderungsrate, …),
• den Auswirkungen von Parametervariation,
• der Wurzelfunktion als Umkehrfunktion,
• der Anwendung in verschiedensten Realsituationen.

Mithilfe von dynamischen Arbeitsblättern können experimentell die Eigenschaften von Wurzelfunktionen erarbeitet werden. Viele Anwendungsbeispiele aus unterschiedlichsten Kontexten dienen einerseits der Festigung des Gelernten, zeigen den Schüler/innen aber auch, in welchen Bereichen Wurzelfunktionen benötigt werden (Sichtweite, Bremsweg, Blutvolumen in den Adern,…).

Der Lernpfad unterteilt sich in 7 Phasen, wobei Phase 1 - 4 (beschäftigen sich mit der Quadratwurzelfunktion) auf alle Fälle bearbeitet werden sollen. Phase 5 – 7 können fakultativ bearbeitet werden, da sie als Erweiterung bzw. als Vertiefung dienen. Mögliche Verzweigungen innerhalb des Lernpfads sind am Ende jeder Phase durch Links gekennzeichnet.

Phase 1 (Die Wurzelfunktion):

Das Vorwissen zum Rechnen mit Potenzen kann anhand von drei Übungen aktiviert werden. Dann erarbeiten die Schüler/innen eine formelhafte, tabellarische und graphische Darstellung der Quadratwurzelfunktion und stellen Überlegungen zur Definitionsmenge und Wertemenge an.

Phase 2 (Übungen):

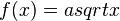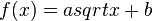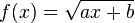Die Inhalte aus Phase 1 können geübt und vertieft werden. Außerdem lernen die Schüler/innen mit Hilfe von Applets die Auswirkun'gen von Parametern in Wurzelfunktion der Form $f(x) = a sqrt x$, $f(x) = a sqrt x + b$ und $f(x) = \sqrt{ax+b}$ kennen.

Phase 3 (Anwendungen):

Drei Beispiele verdeutlichen den Schüler/innen den Einsatz von Wurzelfunktionen in verschiedenen Anwendungssituationen. Das bisher Gelernte wird geübt und weiter vertieft.

Phase 4 (Weitere Eigenschaften):

Der Differenzenquotient mit seinen verschiedenen Verwendungsmöglichkeiten (Steigung der Sekante, Berechnung des Steigungswinkels, mittlere Änderungsrate) wird auf die Wurzelfunktion angewendet.

Phase 5 (Die allgemeine Wurzelfunktion):

Die Schülern/innen erarbeiten eine formelhafte, tabellarische und graphische Darstellung der allgemeinen Wurzelfunktion $f(x) = \sqrt[n]{x}$ und stellen Überlegungen zur Definitionsmenge und Wertemenge an.

Phase 6 (Übungen und Anwendungen): Die bisher kennengelernten Eigenschaften der allgemeinen Wurzelfunktion $f(x) = \sqrt[n]{x}$ werden geübt und in unterschiedlichen Kontexten angewendet.

Phase 7 (Die Wurzelfunktion als Umkehrfunktion):

Der in den Einstiegsbeispielen in Phase 1 und Phase 5 bereits behandelte Zusammenhang zwischen Potenzfunktionen und Wurzelfunktionen wird wieder aufgegriffen und durch Einführung des Begriffs der Umkehrfunktion exaktifiziert. Die Schüler/innen lernen den graphischen Zusammenhang von Funktion und Umkehrfunktionen kennen. Sie lernen das Ermitteln der Funktionsgleichung einer Umkehrfunktion, sowie die Beziehung von Definitionsmenge und Wertemenge von Funktion und Umkehrfunktion kennen.

Kurzinformation

Schulstufe	10. Schulstufe
Dauer	4 - 5 Stunden, es können aber auch einzelne Phasen ausgelassen werden.
Unterrichtsfächer	Mathematik
Verwendete Medien	Java Applets, Internet
Autor/innen	Irma Bierbaumer, Karl Haberl, Evelyn Süss-Stepancik

Voraussetzungen

• Technische Voraussetzungen : Java (kostenlos von www.java.com), Internet
• Technisches Vorwissen: Elementarer Umgang mit dem Computer, Verwendung von dynamischen Applets
• Vorwissen der Schüler/innen: Potenzfunktionen, Rechnen mit Wurzeln, verschiedene Darstellungsformen von Funktionen (Tabelle, Graph, Term).

Lerninhalte und Lernziele

Lerninhalt	Lernziele
Wurzelfunktionen	Wurzelfunktionen definieren, darstellen und untersuchen können. Eigenschaften reeller Funktionen und von Beziehungen zwischen Funktionen (Umkehrfunktionen) beschreiben können. Änderungen durch Änderungsmaße (absolute und relative Änderung, Differenzenquotient) beschreiben können. Funktionen zur Beschreibung kontinuierlicher Prozesse anwenden können.

Genderaspekte

In folgenden Bereichen wurden Genderaspekte berücksichtigt:

Es werden/ es wird

Inhalt und Material

• an den Interessen beider Geschlechter angeknüpft
• geschlechtssensitive bzw. geschlechtsneutrale Bilder verwendet

Genderbewusste Sprache

• eine genderbewusste Sprache in allen Texten und Aufgaben verwendet
• in der Sprache und beim Sprechen beide Geschlechter sichtbar gemacht und / oder geschlechtsneutrale Begriffe verwendet
• weibliche und männliche und / oder geschlechtsneutrale Sprachformen verwendet

Genderansätze in den Lernmaterialien

• interaktive (Experimentier-)Anteile eingesetzt
• kreative Lernfortschrittsüberprüfungen angeboten
• verschiedene Lerntypen angesprochen
• verschiedene Sozialformen eingesetzt
• die mathematischen Inhalte schrittweise exaktifiziert

Kompetenzen

Folgende Handlungsdimensionen kommen im Lernpfad vor:

Darstellen und Modellbilden:

• einen gegebenen mathematischen Sachverhalt in eine andere Darstellungsform übertragen (im gesamten Lernpfad)
• geeignete mathematische Mittel (Begriffe, Modelle, Darstellungsformen, Technologien) und Lösungswege auswählen (im gesamten Lernpfad)
• aus bekannten (z. B. auch elektronisch verfügbaren) mathematischen Modellen neue Modelle entwickeln (im gesamten Lernpfad)
• ein für die Problemstellung geeignetes mathematisches Modell verwenden oder entwickeln (Phase3 – Anwendungen, Phase 6 – Übungen und Anwendungen)

Rechnen und Operieren:

• mit und in Tabellen oder Grafiken operieren (gesamter Lernpfad)
• mit Formeln operieren (gesamter Lernpfad)

Interpretieren:

• Werte aus Tabellen oder grafischen Darstellungen ablesen, sie im jeweiligen Kontext deuten (im gesamten Lernpfad)
• tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge beschreiben und im jeweiligen Kontext deuten (im gesamten Lernpfad)

Argumentieren und Begründen:

• mathematische Zusammenhänge herleiten (im gesamten Lernpfad)

Einsatz im Unterricht

Grundsätzlich ist für ein effizientes Arbeiten pro Schüler/in ein PC empfehlenswert, allerdings ist auch eine Partner/innenarbeit an einem Gerät bei entsprechender Abstimmung der Lerngeschwindigkeiten der beiden Partner/innen durchaus möglich.

Die meisten Aufgabenstellungen bearbeiten die Schüler/innen alleine bzw. in Partner/innenarbeit am Computer. In Phase 2 (Übungen) findet sich ein Vorschlag zur Gruppenarbeit, um 3 ähnliche Aufgabenstellungen mit der Methode des „Gruppenpuzzles“ zu bearbeiten. Das Ergebnis der Gruppenarbeit wird in Mischgruppen präsentiert und die Mischgruppe bearbeitet 3 weitere Problemstellungen, deren Lösungen dann im Plenum vorgestellt werden.

Dieser Lernpfad ist in sieben Teilen aufgebaut, wobei die Teile 1 - 4 (beschäftigen sich mit der Quadratwurzelfunktion) auf alle Fälle bearbeitet werden sollen.
Die Teile 5 – 7 können fakultativ bearbeitet werden, da sie als Erweiterung bzw. als Vertiefung dienen. Mögliche Verzweigungen innerhalb des Lernpfads sind am Ende jeder Phase durch Links gekennzeichnet.

Zusätzliches Arbeitsmaterial wie Arbeitsblätter können von den Schüler/innen auch selbst ausgedruckt werden, da diese sich direkt im Lernpfad befinden.

Kombination der Medien

In dem vorliegenden Lernpfad wird versucht, durch den Einsatz von interaktiven Applets, die mit der Software GeoGebra erstellt wurden, das selbsttätige Lernen der Schüler/innen zu fördern. Die neu gewonnenen Erkenntnisse sollen auch durch händisches Zeichnen im Koordinatensystem und durch eine sorgfältige Dokumentation unterstützt werden.

Lernmedien der Schüler/innen

Die Schüler/innen arbeiten mit diesem Lernpfad nicht nur am Computer. Ihre Tätigkeiten und Ergebnisse müssen genau dokumentiert und entweder im Schulübungsheft oder in einer Projektmappe festgehalten werden.

Leistungsfeststellung/Leistungsbeurteilung

Nicht nur die Ergebnisse, sondern der Lernprozess, also der Grad der Selbsttätigkeit und die Selbstorganisation, stehen im Zentrum. Für die Leistungsbeurteilung können daher das Engagement der Schüler/innen sowie die Art und Weise der Dokumentation herangezogen werden.

Anleitungen für Lehrer/innen

Die Schüler/innen können den Lernpfad selbständig durchführen, es muss jedoch vorher festgelegt werden, in welcher Form die Dokumentation (ins Schulübungsheft oder in eine Projektmappe) zu erfolgen hat. Bei jedem Lernschritt wird am Ende der Seite eine Kontrolle (Lösung) zu jeder Aufgabenstellung bereitgestellt.

Was hat der Lehrer/ die Lehrerin vor Beginn des Lernpfads zu tun:

• Festlegen, welche Phasen des Lernpfads von den Schüler/innen verpflichtend bzw. welche Phasen freiwillig (als Bonus) zu bearbeiten sind (eventuell auch: welche Phasen ausgelassen werden können) und dies den Schüler/innen kommunizieren.
• Festlegen, wie viel Zeit den Schüler/innen für das Projekt zur Verfügung steht.
• Festlegen, in welcher Form die Dokumentation zu erfolgen hat und wie diese in die Beurteilung mit einfließt.
• Prozedere zur Gruppeneinteilung in Phase 2 (Übungen) überlegen.
• Arbeitsblatt aus Phase 7 (Wurzelfunktion als Umkehrfunktion) ausdrucken und vervielfältigen. Das Arbeitsblatt kann aber auch von den Schüler/innen selbst ausgedruckt werden.
• Hausübung während des Projekts festlegen und den Schüler/innen mitteilen.
• Zur Bearbeitung des Arbeitsblattes in Phase 7 (Wurzelfunktion als Umkehrfunktion) benötigen die Schüler/innen zur Herstellung des Faltbildes entweder Tinte, Wasserfarben oder einen Stift mit sehr flüssiger Farbe. Dies muss den Schüler/innen früh genug mitgeteilt werden.
• In Phase 3 bei Aufgabe 13 benötigen die Schüler/innen zum Anschauen des Videos Kopfhörer. Sollten an der Schule genügend Kopfhörer vorhanden sein, so müssen diese rechtzeitig organisiert werden. Sonst muss den Schüler/innen mitgeteilt werden, dass diese ihre eigenen Kopfhörer mitbringen.

Nach Abschluss des Lernpfades sollte die Dokumentation der Schüler/innen kontrolliert und korrigiert werden.

---

Der didaktische Kommentar kann als pdf-Datei heruntergeladen werden.

---

Zurück zur Startseite: Wurzelfunktionen