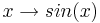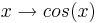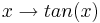Version vom 28. Januar 2011, 15:59 Uhr

Das Bogenmaß

Auf dieser Seite kannst du dich über das Bogenmaß informieren und hier ist ein Rechner zum Umrechnen.

Sinus, Kosinus und Tangens am Einheitskreis

Hier kannst du dich noch einmal informieren wie Sinus und Kosinus am Einheitskreis erklärt sind.
Prüfe deine Kenntnisse auf dieser Seite. In diesem Applet kannst du deine Kenntnisse für sin, cos, tan nochmals wiederholen. Ziehe mit der Maus den Punkt P auf der Kreislinie.

Die trigonometrischen Funktionen

In diesem Applet sieht du wie die Sinusfunktion im Grundintervall [0;2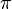] entsteht. Ziehe dabei den blauen Punkt auf dem Einheitskreis mit der Maus und achte darauf, was am rechten Graph passiert.

Merke: Die Funktion   , die jeder reellen Zahl x den Wert sin(x) zuordnet heißt Sinusfunktion .

Das gleiche machst du in diesem Applet für die Kosinusfunktionim Grundintervall [0;2] .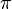

Merke: Die Funktion   , die jeder reellen Zahl x den Wert cos(x) zuordnet heißt Kosinusfunktion .

Merke: Die Funktion   , die jeder reellen Zahl x den Wert tan(x) zuordnet heißt Tangensfunktion .

In diesem Applet ist die Entstehung alle drei Funktionen sin, cos und tan im Grundintervall [0; 2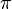] durch "Abwickeln" der Werte am Einheitskreis dargestellt.

Überblick

Einen abschließenden Überblick gibt es auf der Seite:
Die Winkelfunktionen im Überblick und hier kannst du dir die einzelnen Funktionen noch einmal eigens ansehen.

Die Eigenschaften der trigonometrischen Funktionen sin, cos und tan sind hier aufgeführt.

Zurück zur Startseite