Eigenschaften von Funktionen: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(→Monotonie) |
(→Monotonie) |
||
| Zeile 18: | Zeile 18: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
Alle drei Funktionsgraphen "steigen" in dem angegebenen Intervall an.}} | Alle drei Funktionsgraphen "steigen" in dem angegebenen Intervall an.}} | ||
| + | |||
| + | Dieser Begriff des Ansteigens eines Funktionsgraphen fassen wir genauer und benennen ihn. | ||
| + | |||
| + | {{Merke| | ||
| + | Eine Funktion <math> f</math> heißt '''streng monoton steigend''' im Intervall [a;b], wenn für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) < f(x_2)</math> | ||
| + | }} | ||
=Grenzwert= | =Grenzwert= | ||
Version vom 30. Dezember 2011, 14:47 Uhr
Monotonie
|
Betrachte die folgenden Funktionen im angegebenen Intervall. Die Funktionen sind durch Funktionsterm und Graph gegeben. Was fällt dir auf? Was haben die drei Funktionsgraphen in den angegebenen Intervallen gemeinsam? |
Alle drei Funktionsgraphen "steigen" in dem angegebenen Intervall an.
Dieser Begriff des Ansteigens eines Funktionsgraphen fassen wir genauer und benennen ihn.
|
Eine Funktion |
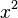 in
in 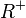
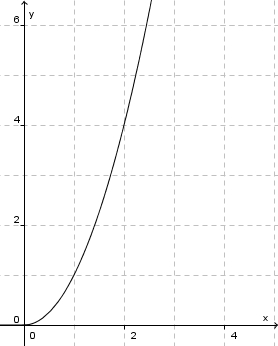
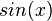 in [0;1]
in [0;1] 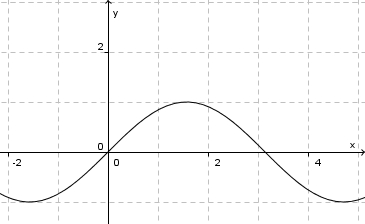
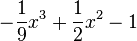 in [0;3]
in [0;3] 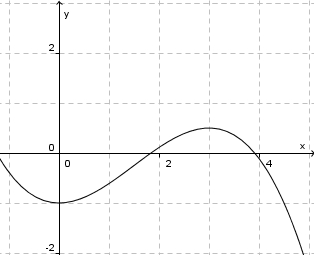
 heißt streng monoton steigend im Intervall [a;b], wenn für alle
heißt streng monoton steigend im Intervall [a;b], wenn für alle ![x_1,x_2 \in [a;b]](/images/math/4/8/9/489a4ad3c2410297428c10a130e7cc95.png) gilt:
gilt: