Wurzelfunktion Übungen 1: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 34: | Zeile 34: | ||
# <math> a = 2;\; 3;\; 4;\; 5;\; 6;\; ...</math> | # <math> a = 2;\; 3;\; 4;\; 5;\; 6;\; ...</math> | ||
# <math> a = 3 \sqrt 2</math> | # <math> a = 3 \sqrt 2</math> | ||
| + | }} | ||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=3| ARBEIT= | ||
| + | Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann man bei guten Bedingungen durch die Formel <math> s = 3,57 \sqrt h</math> (vgl. [http://de.wikipedia.org/wiki/Sichtweite#Berechnung Sichtweite]) beschreiben. Dabei ist h die Augenhöhe in m und s die Sichtweite in km. Dabei geht man am besten von der Sichtweite auf dem Meer aus, da dort keine Berge stören. Ansonsten nimmt man die Kugelgestalt der Erde ohne Berge. | ||
| + | # Zeichne den Graphen zur Funktion <math> s: h \rightarrow 3,57 \sqrt h</math>. | ||
| + | # Wie weit kann man bei einer Augenhöhe von 1,7m bei klarem Wetter sehen. Löse graphisch und rechnerisch. | ||
| + | # Wie weit kann man von der obersten Plattform des [http://de.wikipedia.org/wiki/Eiffelturm Eiffelturms] (276m), vom [http://de.wikipedia.org/wiki/Mount_Everest Mount Everest] (8848m), von der [http://de.wikipedia.org/wiki/Internationale_Raumstation ISS] (380km) sehen? | ||
| + | # Wie hoch muss ein Berg sein, damit man 100km weit sehen kann? | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | # 4,65km | ||
| + | # 59,3km, 335,8km, 2200km | ||
| + | # 786m | ||
}} | }} | ||
Version vom 27. Januar 2012, 18:52 Uhr
|
Im Applet ist der Graph der Wurzelfunktion Wie ändert sich der Graph der Wurzelfunktion
|
|
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
|
|
Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann man bei guten Bedingungen durch die Formel
|
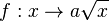 mit
mit  dargestellt.
dargestellt. für
für
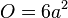
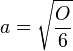
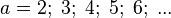
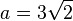
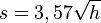 (vgl.
(vgl. 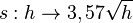 .
.

