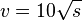Wurzelfunktion Anwendungen: Unterschied zwischen den Versionen
| Zeile 61: | Zeile 61: | ||
[[datei:Parabelbrems.gif|right]] | [[datei:Parabelbrems.gif|right]] | ||
Bei den [http://wikis.zum.de/medienvielfalt/Quadratische_Funktionen_2 quadratischen Funktionen] hast du kennengelernt, dass der Bremsweg s in m eines Autos, welches mit der Geschwindigkeit v in <math> \frac{km}{h}</math> fährt, mit der Faustregel <math> s = (\frac {v}{10})^2</math> berechnet werden kann. | Bei den [http://wikis.zum.de/medienvielfalt/Quadratische_Funktionen_2 quadratischen Funktionen] hast du kennengelernt, dass der Bremsweg s in m eines Autos, welches mit der Geschwindigkeit v in <math> \frac{km}{h}</math> fährt, mit der Faustregel <math> s = (\frac {v}{10})^2</math> berechnet werden kann. | ||
| + | |||
| + | Löse die Gleichung <math> s = (\frac {v}{10})^2</math> nach v auf. | ||
| + | |||
Mit welcher Geschwindigkeit v in <math> \frac{km}{h}</math> ist wohl ein Auto, das eine Bremsspur von | Mit welcher Geschwindigkeit v in <math> \frac{km}{h}</math> ist wohl ein Auto, das eine Bremsspur von | ||
# 20m, | # 20m, | ||
| Zeile 67: | Zeile 70: | ||
# 80m, | # 80m, | ||
# 100m | # 100m | ||
| − | gemacht hat, gefahren? | + | gemacht hat, gefahren?<br> |
| + | Löse graphisch und rechnerisch! | ||
| + | Verwende für die graphische Lösung dieses Applet: | ||
| + | <ggb_applet width="806" height="594" version="4.0" ggbBase64="UEsDBBQACAAIALpaPEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIALpaPEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVjbbtw2EH1OvmKgp6SIvaIoStpgN0GTomgAJyngtCj6RkncXca6RaT2EuTjOyQlrdZ2HOfSFohNUhzO5cyZIZ3F831ZwFa0StbV0iPnvgeiyupcVuul1+nVWeI9f/ZwsRb1WqQth1XdllwvvdBIynzpJYmY8zTzz1YJz8/CPMQjWe6fMZGmcbBiQURREvZKPq3qN7wUquGZuMw2ouQXdca1NbzRunk6m+12u/PB1HndrmfrdXq+V7kH6Galll4/eYrqTg7tqBUPfJ/M/np94dSfyUppXmXCAxNCJ589fLDYySqvd7CTud6g9yT0YCPkeoMxxUHgwcwINQhIIzItt0Lh0cnSxqzLxrNivDL7D9wMijEcD3K5lblol55/ThLGfBqNvz2oWykq3cuS3uZs0LbYSrFzas3MWkQvdV0XKTca4dMnCPzAhydmIG4IcIgit+W7bz51Q+CG0A3MyYTueOhEQycTOpmQerCVSqaFWHorXihEUFarFrM3rpU+FML60384Rk+eYExKfkRh6mPyHeT43fefmJ8If0KzMTsNkkys6rb7SqODycSP7m8y+K5A6WCTMHLTZsA+E2Z0h1EX933iJGwCLZqy/+zPDYv0rjCvW3Tr7zMYhf9JiIvZUCqLvjpAbYxszx4tSmXqhc6BzQ3tCTCsjShGljMgcxziALAagDAIGS5JApEZY6AxboRAIQEjRyjY4mAJ/gpjqywChsrM1xhrEggaCoFRILamQsBKAluXWKMBRQnGgOEhY54ERgWNIIxwRRMI0UdTkjFBQYoHcY3mA6AEqDlMYggiiIw+EppSjxLjOqoMIPIhIkYhVjVWtKtmlE+AmmiiHi5ZNZ0+gSgr82Gq62bMBUpjPzp2PdefTprig0XBU1HgPXFpMgmw5YWpCGtoVVcahiQG7tu65c1GZupSaI2nFLznW37Btdj/itJqsG1ls7pSv7e1flkXXVkpgKwu/NHnuiCTeTB6jQs62QinG2yyEU3m8a12a9yBTgm0X7dqEOd5/spIHFsDIvm2Kg4vWsGvmlqehrGY2StnIbqskLnk1Z9IVmPF4ALjDWTa1XADsSgaHKnb/PKgkMGw/1u0NV4ByTmlbM7CmAYJo2SO5w5ui4XBOSWUkjhkoR+EMbqWcVN77DwIgzjEK8j355TROZ65fSuYO8tiOyaI78UY+7qV+XT+Sr2oi3xEwgb/kje6a+3LATtja0L6uVoXwhLE9lq8lrOrtN5fOmZQp+vdocGV7+ynaws6YGMIzF257sfUjVbGODZK+VbGtxL+QDWZj/tkHlgJO6ZutFLIXedaHygZoiT+YEYq285876RoLPHNJd9VUl8MCy2zqz5S4uTfdGUqjvQxAr9I9yJxT61TK+Tfs7KYXSPh4kq0lSh6zmO6u7pTroQn5ZCLTJa4dBs9bNyk9A/0yX3NxboVvTwv7MvNgWp3/Smdb3y2qn5t6/JVtX2HfLnmwGI2eLlQWSsbw0pI8Z64Ekfm5VJxvGby6TlTpIhGZq4TBEQbtLB8O72pW/s4w66Do6nNQpT4FANtKVh1pWhlNmKv7CsPnep6v0N/yJpBHur0PfbDawmzCyuD259hKfCi2XD7OOy5yA+iPcHGantd573lXk4V5lUJpaysmpLv7XsDFaYKe6XGhzVmozo+rJ1rfa9BSfNs35sL2s4OWKlzM1nJ/QRThEl+RFrwk3CO9aKxj1/hY1XZotZ9+drJbzLPRTX6yyskkE0DtjK8X7CQ8Q4Rju3jwQbDt21jkvo+MyZH+6ZFW0ZJD3GKf6TsUdselqAGPcY9d3OdJtV9H0/+yOT5dybv7WqlhDZoB5GFmt2VWVsiykiTPjM2Qx+X3tmRdd+SAvGhckeUaxuybAqZSf0lmAHT0eO8erR/jFDjA+cnUB9ajUvvJtCrrrIVN4K5+gLYk07z/WgfAfVvp56ptfuR71twvpuwvAfygCiuHqnHX8VZ/r9wNnEkDO7H2aGbkIGzEcXnBWOMBj6lUczmP47AiOStBJ5N2759fvX/k/DsH1BLBwgBRARt8gUAAOYQAABQSwECFAAUAAgACAC6WjxA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIALpaPEABRARt8gUAAOYQAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAiQYAAAAA" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
}} | }} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| + | <math> v = 10 \sqrt s</math> | ||
| + | |||
# 44,7 <math> \frac{km}{h}</math> | # 44,7 <math> \frac{km}{h}</math> | ||
# 63,2 <math> \frac{km}{h}</math> | # 63,2 <math> \frac{km}{h}</math> | ||
| Zeile 77: | Zeile 85: | ||
# 100 <math> \frac{km}{h}</math> | # 100 <math> \frac{km}{h}</math> | ||
}} | }} | ||
| + | |||
| + | |||
---- | ---- | ||
| + | |||
Zurück zu [[Wurzelfunktion_Einführung|Wurzelfunktion]] oder weiter mit [[Wurzelfunktionen_Übungen_1|Übungen]]. | Zurück zu [[Wurzelfunktion_Einführung|Wurzelfunktion]] oder weiter mit [[Wurzelfunktionen_Übungen_1|Übungen]]. | ||
Version vom 28. Januar 2012, 12:23 Uhr
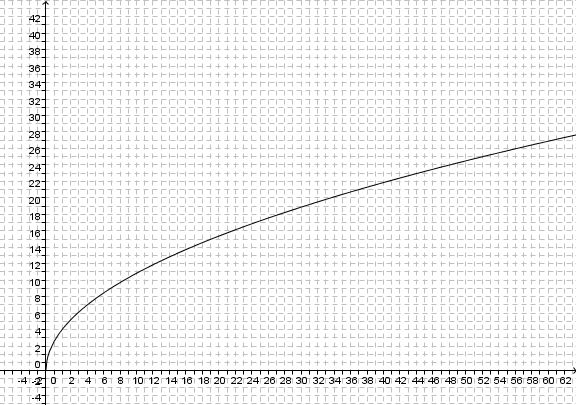
Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher wird zuerst die Funktion 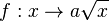 betrachtet.
betrachtet.
|
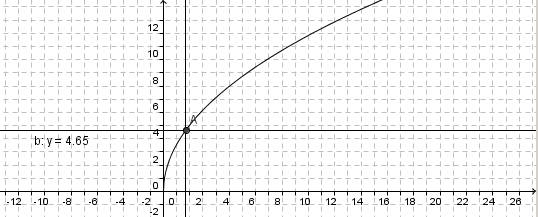
Im Applet ist der Graph der Wurzelfunktion Wie ändert sich der Graph der Wurzelfunktion
|
|
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
|
|
Schau dir diesen Video an. Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann man bei guten Bedingungen durch die Formel
|
|
Bei den quadratischen Funktionen hast du kennengelernt, dass der Bremsweg s in m eines Autos, welches mit der Geschwindigkeit v in Löse die Gleichung Mit welcher Geschwindigkeit v in
gemacht hat, gefahren? |
Zurück zu Wurzelfunktion oder weiter mit Übungen.
 dargestellt.
dargestellt. für
für
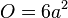
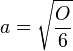
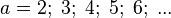
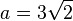
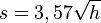 (vgl.
(vgl. 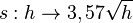 .
.

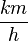 fährt, mit der Faustregel
fährt, mit der Faustregel 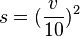 berechnet werden kann.
berechnet werden kann.