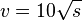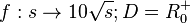Wurzelfunktion Anwendungen: Unterschied zwischen den Versionen
| Zeile 40: | Zeile 40: | ||
</div> | </div> | ||
| − | Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann | + | Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann bei guten Bedingungen näherungsweise durch die Formel <math> s = 3,57 \sqrt h</math> (vgl. [http://de.wikipedia.org/wiki/Sichtweite#Berechnung Sichtweite]) beschreiben werden. Dabei ist <mtah>h</math> die Augenhöhe in m und <math>s</math> die Sichtweite in km. |
| + | <br>Am besten gehst du von der Sichtweite auf dem Meer aus, da dort keine Berge stören. | ||
| + | <br>Ansonsten nimmt du die "ideale" Kugelgestalt der Erde ohne Berge und Täler. | ||
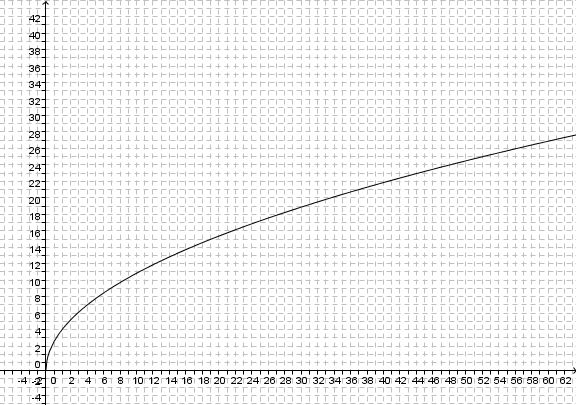
# Zeichne den Graphen zur Funktion <math> s: h \rightarrow 3,57 \sqrt h</math>. | # Zeichne den Graphen zur Funktion <math> s: h \rightarrow 3,57 \sqrt h</math>. | ||
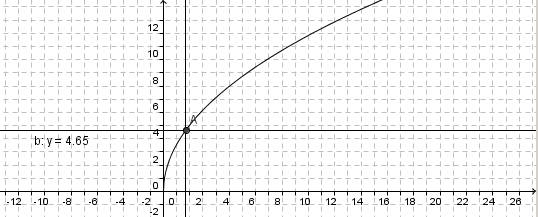
# Wie weit kann man bei einer Augenhöhe von 1,7m bei klarem Wetter sehen. Löse graphisch und rechnerisch. | # Wie weit kann man bei einer Augenhöhe von 1,7m bei klarem Wetter sehen. Löse graphisch und rechnerisch. | ||
Version vom 28. April 2012, 14:27 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher betrachten wir zuerst die Funktion 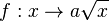 .
.
|
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
|
|
Schau dir dieses Video an. Wie weit kannst du bis zum Horizont sehen? Etwa MIt welcher Formel kannst du die Sichtweite a berechnen? Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann bei guten Bedingungen näherungsweise durch die Formel
|
|
Bei den quadratischen Funktionen hast du kennengelernt, dass der Bremsweg s in m eines Autos, welches mit der Geschwindigkeit v in
a) 20m, |
Zurück zu Wurzelfunktion oder weiter mit Übungen.
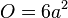
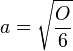
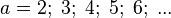
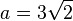
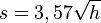 (vgl.
(vgl.  die Sichtweite in km.
die Sichtweite in km.
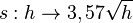 .
.

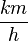 fährt, mit der Faustregel
fährt, mit der Faustregel 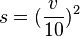 berechnet werden kann.
berechnet werden kann.
 mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.
mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.