Wurzelfunktion allgemeine Wurzelfunktion: Unterschied zwischen den Versionen
| Zeile 25: | Zeile 25: | ||
b) Gib eine Funktionsgleichung an, die der Seitenlänge <math>a</math> das Volumen <math>V</math> eines Würfels zuordnet! | b) Gib eine Funktionsgleichung an, die der Seitenlänge <math>a</math> das Volumen <math>V</math> eines Würfels zuordnet! | ||
c) Welchen Wert nimmt <math>V</math> für <math>a</math> = 3; 5; 10; 15 an? Verwende dazu deine Funktionsgleichung!<br> | c) Welchen Wert nimmt <math>V</math> für <math>a</math> = 3; 5; 10; 15 an? Verwende dazu deine Funktionsgleichung!<br> | ||
| − | + | d) Stelle mit dem Schieberegler für das Volumen <math>V</math> die Werte ein 1,728; 2,744; 3,375; 4,096; 4,913; 9,261; 15,625; 17,576. Lies die dazugehörigen Seitenlängen <math>a</math> im Applet ab und ergänze deine Tabelle! | |
}} | }} | ||
Version vom 28. April 2012, 13:51 Uhr
Startseite --- Die Wurzelfunktion - Übungen - Anwendungen --- Die allgemeine Wurzelfunktion - Übungen - Anwendungen --- Die Wurzelfunktion als Umkehrfunktion
Bei den folgenden Aufgaben bearbeitest du den Zusammenhang zwischen dem Volumen eines Würfels und seiner Seitenlänge.
Ein Würfel mit der Seitenlänge  hat das Volumen
hat das Volumen 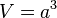 .
.
Ist die Seitenlänge 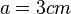 , dann ist also das Volumen
, dann ist also das Volumen 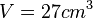 .
.
Umgekehrt ist dann für einen Würfel mit Volumen 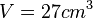 die zugehörige Seitenlänge
die zugehörige Seitenlänge 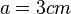 .
.
|
Im folgenden Applet wird der Seitenlänge
a) Welches Volumen |
a) a, 3,375; 8; 15,625
b) 27; 125; 1000; 3375
c) 1,2; 1,4; 1,5; 1,6; 1,7; 2,1; 2,5; 2,6
Es ist
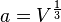
Man schreibt auch dafür
|
Merke:
Die Gleichung 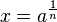 oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\ oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\
Fehler beim Parsen(Lexikalischer Fehler): \sqrt[n]{a}\ heißt die n-te Wurzel aus a. |
|
a) Setze verschiedene Werte für das Würfelvolumen V ein, und berechne welche Werte sich für die Seitenlänge a ergeben. Trage die Ergebnisse in eine Wertetabelle ein. b) Erstelle ein V-a-Diagramm (V nach rechts, a nach oben antragen!) |
|
Merke:
Man definiert für jede natürliche Zahl n die allgemeine Wurzelfunktion n-ten Grades oder n-te Wurzelfunktion Fehler beim Parsen(Lexikalischer Fehler): f: x \rightarrow \sqrt[n]{x}\ mit |
|
Gib für die Würfelaufgabe die zugehörige Funktion an. |
![f:V \rightarrow \sqrt[3]{V}](/images/math/5/6/2/56277ceb06d9f1e85ce77b321e54ee46.png) mit
mit 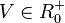
|
1. Stelle mit dem Schieberegler die passende Wurzelfunktion ein.
2. (0;0 und (1;1)
|
Betrachte nun die Wurzelfunktionen im folgenden Applet:
|
- Für ungerade n ist der Funktionsgraph auch für negative x gezeichnet.
- Es ist
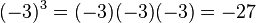 und damit
und damit ![\sqrt[3]{-27}\ = -3](/images/math/7/3/2/7323b20abc6126988a0de2478618344e.png) oder allgemein
oder allgemein 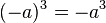 und damit
und damit ![\sqrt[3]{-a^3}\ = -a](/images/math/f/3/8/f389bc623f1322d6697955ebeca3c1d1.png) , also ist bei ungeraden Exponenten n auch die n-te Wurzel aus einer negativen Zahl erklärt.
, also ist bei ungeraden Exponenten n auch die n-te Wurzel aus einer negativen Zahl erklärt.
Du hast nun die allgemeine Wurzelfunktion kennengelernt. Als nächstes kannst du wählen, ob du Übungen oder Anwendungen machen willst.

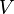 zugeordnet.
zugeordnet. 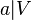 ). Mit dem Schieberegler kannst du verschiedene Werte für
). Mit dem Schieberegler kannst du verschiedene Werte für 
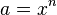 hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung
hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung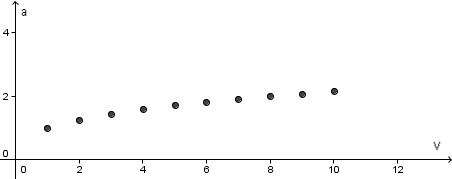
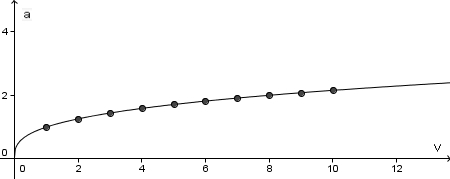
 und
und 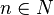 .
.

