Marie: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
</div> | </div> | ||
| − | + | __NOTOC__ | |
===FAQ=== | ===FAQ=== | ||
[[Trigonometrische_Funktionen 2/Zum_Nachschlagen|Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.]] | [[Trigonometrische_Funktionen 2/Zum_Nachschlagen|Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.]] | ||
| − | ==Marie und ihre | + | ==Marie und ihre Freunde== |
| − | Marie hat zwei | + | Marie hat zwei Brieffreunde. Pablo wohnt in Madrid, Maike in Hamburg. In den Sommerferien trafen sie sich in Wien und gingen in den Prater. Dort bestaunten sie das Riesenrad. Maike fiel sofort ein, als sie das Riesenrad sah, dass sie im Mathematikunterricht die Sinusfunktion durch Abwickeln am Einheitskreis erhalten hatte. |
'''Tipp:''' <br> | '''Tipp:''' <br> | ||
| Zeile 17: | Zeile 17: | ||
==Riesenrad== | ==Riesenrad== | ||
| − | Maike meinte nun, dass eine Gondel sicher auch eine Sinuslinie beschreibt. Marie und | + | Maike meinte nun, dass eine Gondel sicher auch eine Sinuslinie beschreibt. Marie und Pablo wollten dies natürlich erklärt haben. Unterstütze sie, indem du Ihnen mit dem folgenden GeoGebra-Applet bei der Lösungsfindung hilfst. |
| Zeile 46: | Zeile 46: | ||
| − | Nachdem Marie, | + | Nachdem Marie, Pablo und Maike im Prater Riesenrad gefahren sind, gingen sie ein Eis essen. Dabei beobachteten sie die Sonne, wie sie gen Westen immer tiefer stand und unterging. Maike bemerkte dabei, dass sie in Hamburg immer ganz lange Sommertage haben. Pablo meinte, dass die Tage in Madrid gar nicht so lang seien. Marie meint nur, dass heute in Wien ein toller Sommertag war. Allerdings beschäftige sie dieses Problem weiter und Marie bat ihre Freunde einmal über ein Jahr hin zu beobachten wie lang die Tage in Hamburg und Madrid seien. Regelmäßig zum Monatsersten notierten sie die Sonnenaufgangs- und Sonnenuntergangszeiten und schrieben Marie die Tageslängen. |
==Tageslänge== | ==Tageslänge== | ||
| Zeile 67: | Zeile 67: | ||
und stellt fest, dass diese Punkte auf einer Sinuslinie liegen. | und stellt fest, dass diese Punkte auf einer Sinuslinie liegen. | ||
| − | Nun möchte sie natürlich Terme für diese Sinuskurven der Tageslängen in Madrid und Hamburg angeben und ihren | + | Nun möchte sie natürlich Terme für diese Sinuskurven der Tageslängen in Madrid und Hamburg angeben und ihren Freunde mitteilen. |
| Zeile 86: | Zeile 86: | ||
---- | ---- | ||
| − | ''' | + | '''Aufgabe 1''' |
| − | + | {{Lösung versteckt|1= | |
| − | + | ||
Die Sinusfunktion schaut im GeoGebra-Applet etwa so aus: | Die Sinusfunktion schaut im GeoGebra-Applet etwa so aus: | ||
[[Bild:Ggb-riesenrad-lsg.jpg]] | [[Bild:Ggb-riesenrad-lsg.jpg]] | ||
| Zeile 95: | Zeile 94: | ||
:# Die Sinusfunktion lautet: x --> 20sin(0,05x - 1,56) + 30 | :# Die Sinusfunktion lautet: x --> 20sin(0,05x - 1,56) + 30 | ||
}} | }} | ||
| − | |||
| − | |||
| − | + | '''Aufgabe 2''' | |
| − | + | ||
| + | {{Lösung versteckt|1= | ||
Amplitude: a = <math> \frac{1}{2}max-min </math><br> | Amplitude: a = <math> \frac{1}{2}max-min </math><br> | ||
Mittelwert: d = min + a<br> | Mittelwert: d = min + a<br> | ||
| Zeile 118: | Zeile 116: | ||
Tageslänge(t) = <math>2,83 \cdot sin(\frac{2\pi}{365}\cdot(t-80))+12,18</math> | Tageslänge(t) = <math>2,83 \cdot sin(\frac{2\pi}{365}\cdot(t-80))+12,18</math> | ||
}} | }} | ||
| − | |||
---- | ---- | ||
Zurück zu [[Trigonometrische Funktionen 2/Anwendungen|Anwendungen]] | Zurück zu [[Trigonometrische Funktionen 2/Anwendungen|Anwendungen]] | ||
Aktuelle Version vom 10. November 2012, 11:45 Uhr
Einführung - Station 1: Einfluss der Parameter - Station 2: Bestimmung der Funktionsgleichung und mehr - Anwendungen
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Marie und ihre Freunde
Marie hat zwei Brieffreunde. Pablo wohnt in Madrid, Maike in Hamburg. In den Sommerferien trafen sie sich in Wien und gingen in den Prater. Dort bestaunten sie das Riesenrad. Maike fiel sofort ein, als sie das Riesenrad sah, dass sie im Mathematikunterricht die Sinusfunktion durch Abwickeln am Einheitskreis erhalten hatte.
Tipp:
1. Falls du nicht mehr weißt wie das "Abwickeln am Einheitskreis" funktioniert, kannst du es hier nochmals anschauen.
2. Informationen zum Riesenrad im Wiener Prater findest du hier.
Riesenrad
Maike meinte nun, dass eine Gondel sicher auch eine Sinuslinie beschreibt. Marie und Pablo wollten dies natürlich erklärt haben. Unterstütze sie, indem du Ihnen mit dem folgenden GeoGebra-Applet bei der Lösungsfindung hilfst.
|
Nachdem Marie, Pablo und Maike im Prater Riesenrad gefahren sind, gingen sie ein Eis essen. Dabei beobachteten sie die Sonne, wie sie gen Westen immer tiefer stand und unterging. Maike bemerkte dabei, dass sie in Hamburg immer ganz lange Sommertage haben. Pablo meinte, dass die Tage in Madrid gar nicht so lang seien. Marie meint nur, dass heute in Wien ein toller Sommertag war. Allerdings beschäftige sie dieses Problem weiter und Marie bat ihre Freunde einmal über ein Jahr hin zu beobachten wie lang die Tage in Hamburg und Madrid seien. Regelmäßig zum Monatsersten notierten sie die Sonnenaufgangs- und Sonnenuntergangszeiten und schrieben Marie die Tageslängen.
Tageslänge
Marie erstellt daraufhin folgende Tabelle:

Dabei bedeutet der Eintrag 9:21, dass der Tag zwischen Sonnenaufgang und Sonnenuntergang 9 Stunden und 21 Minuten lang ist.
Sie macht dazu dieses Diagramm:
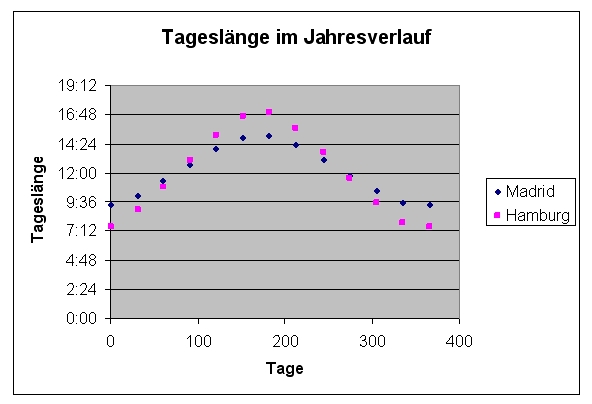
Um eine Idee zu bekommen, auf welcher Linie, die dazwischenliegenden Tage liegen könnten, verbindet sie die Punkte
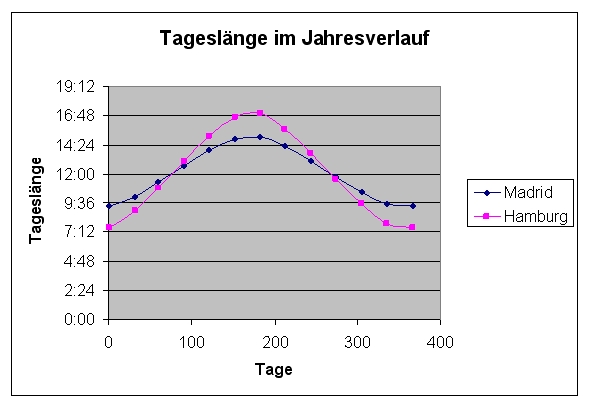
und stellt fest, dass diese Punkte auf einer Sinuslinie liegen.
Nun möchte sie natürlich Terme für diese Sinuskurven der Tageslängen in Madrid und Hamburg angeben und ihren Freunde mitteilen.
|
Aufgabe 1
Die Sinusfunktion schaut im GeoGebra-Applet etwa so aus:
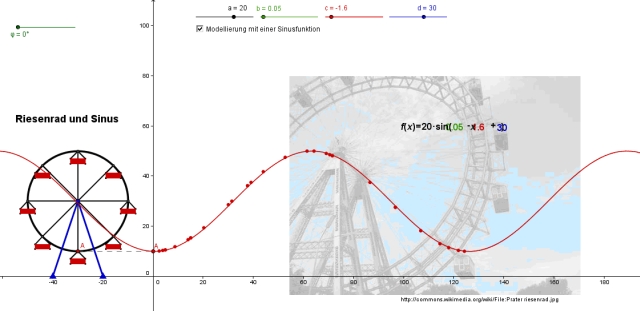
- Die Parameterwerte sind: a = 20, b = 0,05, c = -1,56, d = 30
- Die Sinusfunktion lautet: x --> 20sin(0,05x - 1,56) + 30
Aufgabe 2
Amplitude: a = 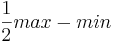
Mittelwert: d = min + a
Periodendauer: T = 365
Verschiebung:80 Die Periode beginnt am 21. März (Tag- und Nachtgleiche), nicht am 1. Januar!
Tageslänge Hamburg:
a: 4:41,5 ergibt als Zahlenwert 4,69
d: 12:15,5 ergibt als Zahlenwert 12,26
Tageslänge(t) = 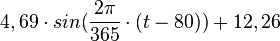
Tageslänge Madrid:
a: 2:50 ergibt als Zahlenwert 2,83
d: 12:11 ergibt als Zahlenwert 12,18
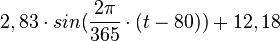
Zurück zu Anwendungen
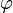 mit dem Schieberegler.
mit dem Schieberegler.

