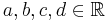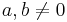Einfluss der Parameter: Unterschied zwischen den Versionen
(Zusatzaufgabe Eselsbrücke) |
(→Station 1: Erforsche den Einfluss der Parameter auf das Aussehen des Graphen!) |
||
| (26 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| − | [[ | + | [[Trigonometrische_Funktionen_2_Startseite|Startseite]] - [[Trigonometrische Funktionen 2/Einfluss der Parameter|Station 1: Einfluss der Parameter]] - [[Trigonometrische Funktionen 2/Bestimmung der Funktionsgleichung aus dem Graphen|Station 2: Bestimmung der Funktionsgleichung und mehr]] - [[Trigonometrische Funktionen 2/Anwendungen_2|Anwendungen]] |
</div> | </div> | ||
| − | + | __NOCACHE__ | |
===FAQ=== | ===FAQ=== | ||
[[Trigonometrische_Funktionen 2/Zum_Nachschlagen|Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.]] | [[Trigonometrische_Funktionen 2/Zum_Nachschlagen|Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.]] | ||
| + | <br> | ||
| + | ===Station 1: Erforsche den Einfluss der Parameter auf das Aussehen des Graphen!=== | ||
| + | |||
| + | <br> | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
| Zeile 15: | Zeile 19: | ||
:#Du erkennst die Auswirkungen auf den Graphen der durch einen Term gegebenen Funktion. | :#Du erkennst die Auswirkungen auf den Graphen der durch einen Term gegebenen Funktion. | ||
:#Du kannst zu gegebenen Funktionstermen die richtigen Graphen finden und selbst zeichnen. | :#Du kannst zu gegebenen Funktionstermen die richtigen Graphen finden und selbst zeichnen. | ||
| + | }}</div> | ||
| + | |||
| + | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
| + | '''Methoden''' | ||
| + | {{versteckt| | ||
| + | :#Falls deine Klasse diese Station in Expertenteams bearbeitet, klicke auf [[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Einteilung_in_ABC-Expertenteams|Einteilung in ABC-Expertenteams]] und nach der Bearbeitung der Tabelle auf [[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Einteilung_in_123-Expertenteams|Einteilung in 123-Expertenteams]]. | ||
| + | :#Wenn deine Klasse diese Station mit der Methode Arbeiten "im Pferdestall" bearbeiten möchte, klicke auf [[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Arbeiten_im_Pferdestall|Arbeiten "im Pferdestall"]]. | ||
| + | :#Ansonsten ignoriere die genannten Links. | ||
}} | }} | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| | {| | ||
| | | | ||
<span style="background-color:yellow;">Hefteintrag:</span> Am besten verwendest du hierfür dein Heft im Querformat, damit du eine Tabelle mit vier Spalten für den Einfluss von <math>\ a,b,c</math> und <math>\ d</math> anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen. | <span style="background-color:yellow;">Hefteintrag:</span> Am besten verwendest du hierfür dein Heft im Querformat, damit du eine Tabelle mit vier Spalten für den Einfluss von <math>\ a,b,c</math> und <math>\ d</math> anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen. | ||
| − | ||{{#ev:youtube|NcVt-bFxu04|150}} | + | ||<!--{{#ev:youtube|NcVt-bFxu04|150}}--> |
|} | |} | ||
---- | ---- | ||
| − | |||
| − | |||
{| | {| | ||
| Zeile 88: | Zeile 93: | ||
:<math> x \rightarrow \cos x + d </math>. | :<math> x \rightarrow \cos x + d </math>. | ||
|} | |} | ||
| − | ||{{#ev:youtube|sSv2C9v6jPc|150}} | + | ||<!--{{#ev:youtube|sSv2C9v6jPc|150}}--> |
|} | |} | ||
| − | |||
| − | |||
---- | ---- | ||
| Zeile 100: | Zeile 103: | ||
| | | | ||
{{Arbeiten|NUMMER=1|ARBEIT= | {{Arbeiten|NUMMER=1|ARBEIT= | ||
| − | Welcher Zusammenhang besteht zwischen der Sinus- und der Kosinusfunktion? Zeichne dazu die Graphen der Funktionen <math>\,\!x \rightarrow \sin\left(x+\frac{\pi}{2}\right)</math> und <math>\,\!x \rightarrow \cos(x)</math> in dein Heft oder mit Hilfe von | + | Welcher Zusammenhang besteht zwischen der Sinus- und der Kosinusfunktion? Zeichne dazu die Graphen der Funktionen <math>\,\!x \rightarrow \sin\left(x+\frac{\pi}{2}\right)</math> und <math>\,\!x \rightarrow \cos(x)</math> in dein Heft oder mit Hilfe von GeoGebra und betrachte sie! Was fällt dir auf? |
:[[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Tipp_zum_Zeichnen_ins_Heft|Tipp zum Zeichnen ins Heft]] | :[[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Tipp_zum_Zeichnen_ins_Heft|Tipp zum Zeichnen ins Heft]] | ||
}} | }} | ||
| − | ||{{#ev:youtube|SQsZVmre3ZI|150}} | + | ||<!--{{#ev:youtube|SQsZVmre3ZI|150}}--> |
|} | |} | ||
| Zeile 121: | Zeile 124: | ||
Dabei sind <math>\ a,b,c,d </math> Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt <span style="background-color:yellow;"> '''<math>\ a,b,c,d \in \R </math>''' </span> und <span style="background-color:yellow;"> '''<math>a,b\neq 0</math>''' </span>.}} | Dabei sind <math>\ a,b,c,d </math> Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt <span style="background-color:yellow;"> '''<math>\ a,b,c,d \in \R </math>''' </span> und <span style="background-color:yellow;"> '''<math>a,b\neq 0</math>''' </span>.}} | ||
| − | ||{{#ev:youtube|NCfr2oh8Kec|150}} | + | ||<!--{{#ev:youtube|NCfr2oh8Kec|150}}--> |
|} | |} | ||
| Zeile 128: | Zeile 131: | ||
{{Arbeiten|NUMMER=2|ARBEIT= | {{Arbeiten|NUMMER=2|ARBEIT= | ||
Bringe den Smily zum Lachen! Variiere dazu die verschiedenen Parameter der allgemeinen Sinusfunktion und beobachte die Auswirkungen auf den Graphen.}} | Bringe den Smily zum Lachen! Variiere dazu die verschiedenen Parameter der allgemeinen Sinusfunktion und beobachte die Auswirkungen auf den Graphen.}} | ||
| − | ||{{#ev:youtube|nzqgoOyNA6w|150}} | + | ||<!--{{#ev:youtube|nzqgoOyNA6w|150}}--> |
|} | |} | ||
| − | + | <center> | |
| − | <ggb_applet | + | <ggb_applet width="690" height="517" version="4.2" ggbBase64="UEsDBBQACAgIADo54kIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIADo54kIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vxbc9u2En5OfwVGT+05EY37pWO346ZNmzS3xunl9KVDkZTEWiIVkrJlTx/OPzx/6SwAUpIlWbFSy3Y5mUkMXgAs8O3ut7uw5MOvZ+MROkuKMs2zow4JcAclWZTHaTY46kyrfld3vv7qs8NBkg+SXhGifl6Mw+qowwPaWYyDu4AwOziNjzox6fdFL+x3VSzCLg9Zr9uL+71uQnHMQkaiqBd2EJqV6ZdZ/iocJ+UkjJKTaJiMwxd5FFZuzmFVTb48ODg/Pw8a6UFeDA4Gg14wK+MOgpVn5VGnvvgSprsy6Jy57hRjcvDbyxd++m6alVWYRUkH2V1N068+e3R4nmZxfo7O07gaHnWk0R00TNLBELYppOqgA9tpAnudJFGVniUlDF26dXuuxpOO6xZm9v0jf4VG8+10UJyepXFSHHVwYAjRRAqluWaUC4AyL9Ikq+q+uJZ50Mx2eJYm535ae+Uk8g6q8nzUC+2MSBj011+IYorRY9sQ31BopPSvsH+GmW+ob7hvhO/D/XDuu3Lfh/s+nIHG0zLtjZKjTj8clQBimvULUOD8vqwuRolbUv1gAQB9DNss00voDPI6yKMOa3+MH3Ps/vttL+2RLEmsiulWgf79krxGmiDyZtLo39ofXshTV+XRa+TpvyWPNPKIWEJT4Mfun/u/jqe8c5FsJ1RXlfgxEiXfItELuF2BHBt1xyIVvguBhwcN7xzWVIPKoe1b+2KVjEtLPsw4/kEECSAZqYAuBCIGGkXhMUVEIC7glmgkbasQU/CCI4Y0sv0IQ45lhIYf3L4jEgmYyz5U2N6DGI4EQ8RxE0fASMjxG3AdZdBDCCRgkJVOrFgmEZdwwzTisEDLbIrY5zAO7kE4RYwgZscShahEkiJl2ZFwS5pS27XDpBRJjKQdCvQI1OhpEUZoxOxuwKkmeZnOaWCYjCZzrTgc02wyrWrs6ufROG5wrPKV7nEenX4zB7t+k4RltdwNosMiBvlocSVEPTochb1kBIH8xFoCQmfhCNyx4yT086xCjRVQ/2xQhJNhGpUnSVXBqBL9GZ6FL8IqmT2F3mUj24l2kfMwmUajNE7D7BcwEzuFnRAtAileBFKujZcS5XkRn1yUYDto9ntS5LAATAJKKGNUEaOwATwv/BsqWCDgsZKMG0m4AMuNQmvzlAeMGq2VVAxjBfEUBl3/zolOzuZbC2dJ2cA/KNJ4+fpZ+U0+iudQT/I0q56Ek2pauKQIomBh93ScDUaJg9ZFDkgvotNePjvxmDI/17uLSWJtwsnvDZ7ko7xAhd0YbGVQtz3fuj52YfNe2PXBrgdulJTG8/fEUNfDtT3ful6gdb+0eqOk2SXBjZi0dERio9aSSzuTOerMOmiapdULf/e//4KNptFpvVnih7yajntgcHMjhg7fpj65somkUFgZyahUBnQv5YpcslHuxRW5HyF1CSXIt8rqt41Lca/+U6e79vrdMKlCm5gJyoTRSgn4aU3IW/uKnR+eJkWWjLw1Z2BQ03xaeveau8ijw2mZvAmr4XEWv00GQA1vQsvOFSzed3Ub8O6eROkYBvrntQpDa14/Axj+aZwMiqTuH45cNuwV7N7iZd9ae+ymelrk42fZ2Tuw3ZWlHh40+zksoyKdWA9BPQgXp8nCCwClEIJNvDwONl/CLiJLfKCJyqqpg8JpNczBOE/S0Vkaoud5GA3TMcwATAK7Q8+noxS4GzzEMsgoGUPeiyrnJ9l0nBRpNDeH2KXUsNpps6FGwdYUUN77E9huxYQWsMLrazwJhaPJ0Omb1P4SXiTFFczcbC/zuBZc9ytHNoNH4xSIvgu+hMbhzDkVCntlPppWUMWAmrJFFePXVjMiwXYDCIZw464u4Eq4uqmfzpI5CwF+6SVY1lUzWTh1BTR9CpVB6ZinqjnGXfyQxnGSzRccZmBZTj9AuBO/YwRBIvEuOB86AQQcuy1ZRa2bD2opaq2WmGKt0VJvVUukLVqiQrdGS2FrtUQ4+SdpaTYpQJqdpka5Dxn4zObpn8++QEcoRP+C9Dn7vAft5zP0bxR98QX8jH1qflXJ/WnmYmRnMdd2jS5lETdRKV5TKdmoUrwFVbEN1evt1yXH83Ufr++rOUO48cZcRrxla5utFf9d5dfJU+lMFSyVaaKlUVJyzLFydksDI5TUBjOuCSSHFBZ6ueShDgub/l+ptPzTlZzspoB+0xJAFRRkhClKNeBqjLkvPJ98CM8Pc+kDgFMERHPMBDPSEK4Ib+DUElOtMDUUqmh2K2hG+XgcZjHK3MnSk7SIoOgF4PKiszjYCLH1fRQSa7EopBZoD+K0at7XFFvPt6YnqCXSaBIWC10lH0eSq5X1gijJBm3RnYnyA+EnSQdJduYAKhGa4brIvMDeWtBl82QGYHV9EUDqR5dkaZFgJ0U6Q8dN/+Om1zHAa0hACMFKC8GENBwI6pjVEo65jdQbKOxYwIsNTufX/T7zWy19uZ2OJ6M0Squ5HkfWIJ9ltn5NXDRbr3hPk2RiDzxeZ++KMCvtr4qulrrXG9Yb56ZXLSpZs6Fvt9vQVV//9iO5k1BvQK59GA7v+ZNywgTmXAvZOLzVH9FUUaIoNntw+Jvp5ftd9PL9J73clV6+20Uv331cbHyIahEBBEXNMGcKa0GpU4sKiGAaG4iMUigm955sPG1FsmHBxJIyopS2v7HGHs0uAdOHHISClWvKDeb63sz8h13M/IfWmLkMOKZg0YoqxgnYemPmRmsNusEECy7p3u38WSvsXAYUyIEzgzFAp7RuzJwqo6gUkEpJrYRF+Z7M/PkuZv68NWZ+l0F2G6I/tsLMCQbghFAcCkUhOVW+eHQncnsqF4+LaMW2f/S14jNfKz5ds/TBrrXi4FOteG2tqE3AhNaCC8mwBldaqxU3mISrFVkz/50Xh9v88EVr/FBwwzXmEpJUQhdnjIYppoSBiK6hw9557WU78BSBlEJiARFaY/vZynn8ZoZASOeSECrx7ZyKbcPzVZvxVAHWBjIiTA0zmu0lG7ouarzwUeOljxqv1qLGcNeoMfwUNa6PGhqYiDAMKTHhkA2zTVFjlcDmJ4wrFPbwgsjrdjjp5mRuTQN757w3rYBzcwkIBTU1BguqMBVQgNzOOcc2NH9qMZprBTW/nQOKm4WQ1z6EvPEh5Ke1EHK6awg5/RRCrv8lFQxkhitONOOMan7jwmOdwB5eBHnbCifVgWCQHWMpiWEcC++kPFBESCIZ4fDK8P0nzSetQFMBbporoSFMEIK5PyoXEECIVlpRKqR23/baE+GtsN1bz3YnazQ3uQHNzZGf3OaHlTbRG/uH0hsPiDZKMmWIMlKZVXrb4FuO3da9ayO72a9ypH1QxA5u9K4VbkRYAFmDYBJzo4WiDScpJqDkxFgYuNz/wcjP7QCTBhysU0CIJRh4SNechAFawygEXQ42SO6Kk955Tvp5jZPe78JJ7z9x0kZOophYUsKaASdpIJe1lGvNtRpKWnGuW6OkX/bvRVuVdWvFjBBESgqlCwbi1k2hDSiDVwlBOcFC7Z+Ufm0FnPZ0URnDORW2GBRU3heev7cGzyuntey+Tr+P/yCtQHT19EKKfSK6+nGA0cUgz1Yi5y8+cv7qzy5+h4Z5uNeyexhOfOcz3/ncd76EBoJA+AfZHmsntfx5BeAmvDby8e2R7xYPR3CgxC451PVGWyYDezdfytkHEorNNrttpTta7cLymi8GmoBTrhSUFlhJA37tLK1LdYClwthgZSDMy+YDvB+jmns+UFlVwvnDUQIPKFGQLwtMGGRLwKze/WFKwhmDWh4ThaGRyn+QsCtlYH8LArkBIcAckrdGLZcPRy2Nb3RNwDSXtogGD8Fa+t9D2o+9S6ohCHLNBCGCq9ZoIdwUWO9LD90t/gEpnVL2iyhUSfttH6cZKgMuBOeMGAHOQZq/B/CPUMzB8hfd3V+/qP8e1Vf/B1BLBwjaLVIxiQsAAD9LAABQSwECFAAUAAgICAA6OeJC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIADo54kLaLVIxiQsAAD9LAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAIAwAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> <br> |
| + | </center> | ||
{| | {| | ||
| Zeile 144: | Zeile 148: | ||
Nullstellen, Extrema und Periode ändern sich, die Wertemenge bleibt aber gleich, falls { b } variiert wird. | Nullstellen, Extrema und Periode ändern sich, die Wertemenge bleibt aber gleich, falls { b } variiert wird. | ||
</quiz>}} | </quiz>}} | ||
| − | ||{{#ev:youtube|zQRGPeb47lM|150}} | + | ||<!--{{#ev:youtube|zQRGPeb47lM|150}}--> |
|} | |} | ||
| Zeile 153: | Zeile 157: | ||
* [[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Applet|Memory]] | * [[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Applet|Memory]] | ||
}} | }} | ||
| − | ||{{#ev:youtube|yNkD56kHAE0|150}} | + | ||<!--{{#ev:youtube|yNkD56kHAE0|150}}--> |
|} | |} | ||
| Zeile 166: | Zeile 170: | ||
{| | {| | ||
| | | | ||
| − | {{Arbeiten|NUMMER= | + | {{Arbeiten|NUMMER=6 - Zusatzaufgabe Eselsbrücke |ARBEIT= |
| − | + | Lisa und Ben haben ein gemeinsames Lieblingsfach – Mathematik. Zusammen haben sie sich folgende Eselsbrücke überlegt: | |
| + | :[[Bild:Merkregel.jpg|300px]] | ||
| + | Dabei stehen die Großbuchstaben für die Parameter <math> \ a, b, c </math> und <math>\ d</math> der allgemeinen Sinusfunktion. Verstehst du, was sie mit ihren Aufzeichnungen meinen? Erkläre mindestens einen Teilbereich deinem Nachbarn! Wenn du die Eselsbrücke hilfreich findest, notiere sie in dein Heft!<br> | ||
}} | }} | ||
|| | || | ||
| Zeile 183: | Zeile 189: | ||
[[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Lösung_zu_Aufgabe_5|Lösung zu Aufgabe 5]] | [[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Lösung_zu_Aufgabe_5|Lösung zu Aufgabe 5]] | ||
| + | |||
| + | [[Trigonometrische_Funktionen 2/Einfluss_der_Parameter/Lösung_zu_Aufgabe_6|Lösung zu Aufgabe 6]] | ||
---- | ---- | ||
<span style="background-color:yellow;">Hefteintrag:</span> Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alle gelb hinterlegten Texte übernommen hast! Beachte, dass in der Lösung zur Aufgabe 1 auch ein Hefteintrag "versteckt" ist! | <span style="background-color:yellow;">Hefteintrag:</span> Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alle gelb hinterlegten Texte übernommen hast! Beachte, dass in der Lösung zur Aufgabe 1 auch ein Hefteintrag "versteckt" ist! | ||
| − | ||{{#ev:youtube|vZY8m7O8y1w|150}} | + | ||<!--{{#ev:youtube|vZY8m7O8y1w|150}}--> |
|} | |} | ||
Aktuelle Version vom 11. Dezember 2020, 08:46 Uhr
Startseite - Station 1: Einfluss der Parameter - Station 2: Bestimmung der Funktionsgleichung und mehr - Anwendungen
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Station 1: Erforsche den Einfluss der Parameter auf das Aussehen des Graphen!
Kompetenzen
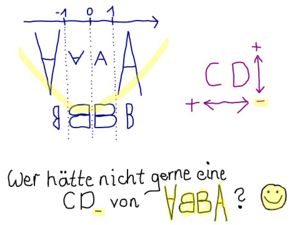
- Auf dieser Seite lernst du welche Bedeutung die Parameter a,b,c und d bei der allgemeinen Sinusfunktion und Kosinusfunktion haben.
- Du erkennst die Auswirkungen auf den Graphen der durch einen Term gegebenen Funktion.
- Du kannst zu gegebenen Funktionstermen die richtigen Graphen finden und selbst zeichnen.
Methoden
- Falls deine Klasse diese Station in Expertenteams bearbeitet, klicke auf Einteilung in ABC-Expertenteams und nach der Bearbeitung der Tabelle auf Einteilung in 123-Expertenteams.
- Wenn deine Klasse diese Station mit der Methode Arbeiten "im Pferdestall" bearbeiten möchte, klicke auf Arbeiten "im Pferdestall".
- Ansonsten ignoriere die genannten Links.
|
Hefteintrag: Am besten verwendest du hierfür dein Heft im Querformat, damit du eine Tabelle mit vier Spalten für den Einfluss von |
|
Jetzt noch was zum Knobeln!!!
|
|
Du hast eine Menge über den Einfluss der einzelnen Parameter auf das Aussehen der Graphen herausgefunden. Natürlich können aber die Parameter nicht nur einzeln variiert werden, sondern auch mehrere oder alle gleichzeitig.
|
|
|
|
|
|
|
|
Hefteintrag: Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alle gelb hinterlegten Texte übernommen hast! Beachte, dass in der Lösung zur Aufgabe 1 auch ein Hefteintrag "versteckt" ist! |
Weiter geht es mit
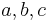 und
und 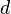 anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
anlegen kannst. Formuliere eine Überschrift und übernimm alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
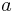
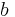

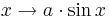
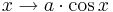 .
.
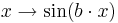
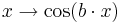 .
.
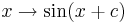
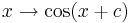 .
.
 .
.
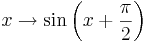 und
und 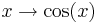 in dein Heft oder mit Hilfe von GeoGebra und betrachte sie! Was fällt dir auf?
in dein Heft oder mit Hilfe von GeoGebra und betrachte sie! Was fällt dir auf?

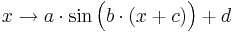
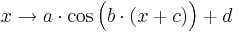
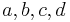 Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt
Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Es gilt