Quadratische Funktionen - Bremsbeschleunigung: Unterschied zwischen den Versionen
(Verlinkung angepasst) |
(Änderung 7616 von Karlo Haberl (Diskussion) rückgängig gemacht.) |
||
| (48 dazwischenliegende Versionen von 8 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Quadratische Funktionen}} | |
| − | + | ||
| − | + | ||
| Zeile 7: | Zeile 5: | ||
Bisher waren wir davon ausgegangen, dass die Länge des Bremsweges lediglich von der Geschwindigkeit abhängt. Das ist in der Realität natürlich nicht der Fall. Bei gleicher Geschwindigkeit hat ein alter LKW auf schneeglatter Fahrbahn selbstverständlich einen ungleich längeren Bremsweg als ein neuer Kleinwagen auf einer trockenen und sauberen Straße. Diese Einflüsse kommen in der sogenannten ''Bremsbeschleunigung'' zum Ausdruck. | Bisher waren wir davon ausgegangen, dass die Länge des Bremsweges lediglich von der Geschwindigkeit abhängt. Das ist in der Realität natürlich nicht der Fall. Bei gleicher Geschwindigkeit hat ein alter LKW auf schneeglatter Fahrbahn selbstverständlich einen ungleich längeren Bremsweg als ein neuer Kleinwagen auf einer trockenen und sauberen Straße. Diese Einflüsse kommen in der sogenannten ''Bremsbeschleunigung'' zum Ausdruck. | ||
| + | |||
Die Bremsbeschleunigung gibt an, wie stark ein Fahrzeug abgebremst wird: Eine hohe Bremsbeschleunigung spricht also für einen kurzen Bremsweg. | Die Bremsbeschleunigung gibt an, wie stark ein Fahrzeug abgebremst wird: Eine hohe Bremsbeschleunigung spricht also für einen kurzen Bremsweg. | ||
| Zeile 13: | Zeile 12: | ||
| | ||
<math>s=\frac{1}{2a_\mathrm{B}}\cdot v^2</math> | <math>s=\frac{1}{2a_\mathrm{B}}\cdot v^2</math> | ||
| − | (s = Bremsweg in m, v = Geschwindigkeit in m/s und a<sub>B</sub> = Bremsbeschleunigung in m/s²). | + | (s = Bremsweg in m, v = Geschwindigkeit '''in m/s''' und a<sub>B</sub> = Bremsbeschleunigung in m/s²). |
| − | In dem folgenden GeoGebra-Applet kann der Bremsweg mit Hilfe der beiden Schieberegler oben links variiert werden | + | In dem folgenden GeoGebra-Applet kann der Bremsweg mit Hilfe der beiden Schieberegler oben links variiert werden. |
| − | + | ||
| − | + | ''Hinweis:'' Der Einfachheit halber wurde der obige Zusammenhang so verändert, dass die Geschwindigkeit in km/h angegeben wird. | |
| − | |||
| + | :::<ggb_applet height="400" width="800" filename="Strassenverhaeltnisse.ggb" /> | ||
| + | |||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
{{Arbeiten| | {{Arbeiten| | ||
NUMMER=1| | NUMMER=1| | ||
ARBEIT= | ARBEIT= | ||
| − | Wie muss a<sub>B</sub> gewählt werden, damit ... | + | Wie muss a<sub>B</sub> gewählt werden, damit ... |
| − | + | #...bei der Geschwindigkeit von 74 km/h der Bremsweg 65 m lang ist? | |
| − | + | #...bei der Geschwindigkeit von 74 km/h der Bremsweg 37 m lang ist? | |
| − | + | #...bei der Geschwindigkeit von 51 km/h der Bremsweg 58 m lang ist? | |
Nutze zur Lösung der Aufgabe das obere Applet. Um die Werte exakt einstellen zu können, klicke den Schieberegler an und verwende dann die Pfeiltasten. | Nutze zur Lösung der Aufgabe das obere Applet. Um die Werte exakt einstellen zu können, klicke den Schieberegler an und verwende dann die Pfeiltasten. | ||
| − | {{Lösung versteckt|1= | + | :{{Lösung versteckt|1= |
| − | + | #a<sub>B</sub> = 3,25 m/s<sup>2</sup> | |
| − | + | #a<sub>B</sub> = 5,71 m/s<sup>2</sup> | |
| − | + | #a<sub>B</sub> = 1,73 m/s<sup>2</sup> | |
| − | + | ||
| − | + | ||
| − | + | ||
}} | }} | ||
| − | |||
}} | }} | ||
| Zeile 52: | Zeile 51: | ||
NUMMER=2| | NUMMER=2| | ||
ARBEIT= | ARBEIT= | ||
| − | Welche Bremsverzögerung liegt vor bei 60%, 75% | + | Welche Bremsverzögerung liegt vor bei |
| + | #60%, | ||
| + | #75% | ||
| + | #100% der Betriebstemperatur der Bremsen? | ||
Entnimm die erforderlichen Größen dem Video. | Entnimm die erforderlichen Größen dem Video. | ||
| − | |||
| − | |||
| − | {{Lösung versteckt|1= | + | :{{Lösung versteckt|1= |
| − | + | ||
| − | + | Geschwindigkeit: v = 100 km/h = (100:3,6) m/s | |
| − | + | Bremswege:< | |
| + | :s(60%) = 49 m | ||
| + | :s(75%) = 47 m | ||
| + | :s(100%) = 37 m | ||
| − | + | Mit Hilfe des Applets von oben erhält man dann: | |
| + | #a<sub>B</sub> = 7,87 m/s<sup>2</sup> | ||
| + | #a<sub>B</sub> = 8,21 m/s<sup>2</sup> | ||
| + | #a<sub>B</sub> = 10,43 m/s<sup>2</sup> | ||
| + | andere Möglichkeit: | ||
| + | Formel nach a<sub>B</sub> auflösen | ||
| + | |||
| + | :<math>a_\mathrm{B}=\frac{v^2}{2}\cdot \frac{1}{s}</math> | ||
| + | |||
| + | dann die Werte einsetzen | ||
| + | |||
| + | Achtung: Die Geschwindigkeit muss dazu in m/s umgerechnet werden! | ||
| + | |||
| + | v = 100 km/h = (100:3,6) m/s | ||
| + | |||
| + | |||
| + | |||
| + | }} | ||
}} | }} | ||
|valign="top"| | |valign="top"| | ||
| Zeile 75: | Zeile 94: | ||
| − | Wenn wir die bisherigen Überlegungen verallgemeinern wollen, müssen wir unsere Gleichung für den Bremsweg genauer analysieren. | + | |
| + | Wenn wir die bisherigen Überlegungen verallgemeinern wollen, müssen wir unsere Gleichung für den Bremsweg genauer analysieren. | ||
| + | |||
Zunächst stellen wir fest, dass es eine funktionale Abhängigkeit des Bremsweges von der Geschwindigkeit gibt; wir können unsere Formel als Funktionsgleichung schreiben: | Zunächst stellen wir fest, dass es eine funktionale Abhängigkeit des Bremsweges von der Geschwindigkeit gibt; wir können unsere Formel als Funktionsgleichung schreiben: | ||
| − | |||
| − | Die rechte Seite der Funktionsgleichung besteht aus dem Vorfaktor <math>\frac{1}{2a_\mathrm{B}}</math> und dem Quadrat der Variablen. Besonders interessant ist dabei der Einfluss des Vorfaktors auf den Verlauf des Graphen: | + | <math>s(v)=\frac{1}{2a_\mathrm{B}}\cdot v^2</math>. Die rechte Seite der Funktionsgleichung besteht aus dem Vorfaktor <math>\frac{1}{2a_\mathrm{B}}</math> und dem Quadrat der Variablen. |
| + | |||
| + | Besonders interessant ist dabei der Einfluss des Vorfaktors auf den Verlauf des Graphen: | ||
| + | |||
| + | |||
{{Arbeiten| | {{Arbeiten| | ||
| Zeile 86: | Zeile 110: | ||
Wie ändert sich der Verlauf des Graphen, wenn der Vorfaktor von v<sup>2</sup>, d.h. wenn <math>\frac{1}{2a_\mathrm{B}}</math> kleiner bzw. größer wird? | Wie ändert sich der Verlauf des Graphen, wenn der Vorfaktor von v<sup>2</sup>, d.h. wenn <math>\frac{1}{2a_\mathrm{B}}</math> kleiner bzw. größer wird? | ||
| − | {{Lösung versteckt|1= | + | :{{Lösung versteckt|1= |
<math>\frac{1}{2a_\mathrm{B}}</math> wird kleiner, wenn a<sub>B</sub> größer wird. Wenn a<sub>B</sub> größer wird, verläuft der Graph flacher. | <math>\frac{1}{2a_\mathrm{B}}</math> wird kleiner, wenn a<sub>B</sub> größer wird. Wenn a<sub>B</sub> größer wird, verläuft der Graph flacher. | ||
Entsprechend wird <math>\frac{1}{2a_\mathrm{B}}</math> größer, wenn a<sub>B</sub> kleiner wird. Wenn a<sub>B</sub> kleiner wird, verläuft der Graph steiler. | Entsprechend wird <math>\frac{1}{2a_\mathrm{B}}</math> größer, wenn a<sub>B</sub> kleiner wird. Wenn a<sub>B</sub> kleiner wird, verläuft der Graph steiler. | ||
}} | }} | ||
| − | |||
}} | }} | ||
| Zeile 97: | Zeile 120: | ||
{|border="0" cellspacing="0" cellpadding="4" | {|border="0" cellspacing="0" cellpadding="4" | ||
| − | |align = "left" width=" | + | |align = "left" width="450"|Die Funktionen, die wir bis jetzt betrachtet haben, weisen eine Gemeinsamkeit auf: Ihr Funktionsterm hat die Form '''ax²'''. Sie zählen daher zu den '''quadratischen Funktionen'''. Die Graphen quadratischer Funktionen unterscheiden sich stark von den Graphen linearer Funktionen. |
| − | + | ||
| − | + | {{Merksatz|MERK= Die Graphen von Funktionen mit der Funktionsgleichung <math>f(x)=ax^2</math> heißen '''Parabeln'''. | |
| + | |||
| + | Sie sind '''symmetrisch zur y-Achse.''' Der Punkt <math>S(0\!\,|\!\,0)</math> heißt '''Scheitel der Parabel''' und ist der tiefste Punkt. | ||
| + | |||
| + | Ist <math>a = 1</math> heißt der Graph '''Normalparabel'''. | ||
| + | }} | ||
| + | <br /> | ||
| + | |||
| + | |||
{{Arbeiten| | {{Arbeiten| | ||
| − | NUMMER= | + | NUMMER=4| |
ARBEIT= | ARBEIT= | ||
| − | Untersuche nun systematisch den Einfluss von a auf den Verlauf des Graphen: | + | Untersuche an dem Applet rechts nun systematisch den Einfluss von a auf den Verlauf des Graphen: |
| − | Was passiert, wenn ... | + | Was passiert, wenn ... |
| − | + | # ... a größer als 1 ist? | |
| − | + | # ... a zwischen 0 und 1 liegt? | |
| − | + | # ... a negativ ist? | |
| − | Vergleiche mit dem Graphen der Funktion g mit g(x)=x². | + | :Vergleiche mit dem Graphen der Funktion g mit g(x)=x². |
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | # Ist a>0, dann ist die Parabel enger (gestreckt) als die Normalparabel. | ||
| + | # Für 0< a < 1 ist die Parabel weiter (gestaucht) als die Normalparabel. | ||
| + | # Ist a negativ, so wird die Parabel an der x-Achse gespiegelt. Sie ist also nach unten geöffnet. | ||
}} | }} | ||
| − | | | + | }} |
| − | | | + | |width=20px| |
| + | |valign="top"|<ggb_applet height="500" width="450" filename="Reinquadratisch.ggb" /> | ||
| − | + | <br> | |
| + | Das Applet zeigt den Graphen einer Funktion f mit '''f(x) = ax²'''. Hierbei steht a für eine beliebige reelle Zahl (<span style="color: darkred">nicht mehr für die Bremsbeschleunigung!</span>). | ||
| − | + | Mit Hilfe des Schiebereglers (unten links im Applet) kannst du den Wert für a variieren. | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
{|border="0" cellspacing="0" cellpadding="4" | {|border="0" cellspacing="0" cellpadding="4" | ||
|align = "left" width="120"|[[Bild:Maehnrot.jpg|100px]] | |align = "left" width="120"|[[Bild:Maehnrot.jpg|100px]] | ||
| − | |align = "left"|'''Als nächstes kannst du prüfen, ob du bis jetzt alles verstanden hast.''' | + | |align = "left"|'''Als nächstes kannst du prüfen, ob du bis jetzt alles verstanden hast.''' |
| + | |||
[[Bild:Pfeil.gif]] [[Quadratische_Funktionen_-_Übungen1|'''Hier geht es weiter''']]'''.''' | [[Bild:Pfeil.gif]] [[Quadratische_Funktionen_-_Übungen1|'''Hier geht es weiter''']]'''.''' | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 22. November 2016, 18:03 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Allgemeine quadratische Funktion - Übungen 3
Unterschiedliche Straßenverhältnisse
Bisher waren wir davon ausgegangen, dass die Länge des Bremsweges lediglich von der Geschwindigkeit abhängt. Das ist in der Realität natürlich nicht der Fall. Bei gleicher Geschwindigkeit hat ein alter LKW auf schneeglatter Fahrbahn selbstverständlich einen ungleich längeren Bremsweg als ein neuer Kleinwagen auf einer trockenen und sauberen Straße. Diese Einflüsse kommen in der sogenannten Bremsbeschleunigung zum Ausdruck.
Die Bremsbeschleunigung gibt an, wie stark ein Fahrzeug abgebremst wird: Eine hohe Bremsbeschleunigung spricht also für einen kurzen Bremsweg.
In einer Formel für den Bremsweg sollte also nicht nur die Geschwindigkeit, sondern auch die Bremsbeschleunigung berücksichtigt werden. In Lehrbüchern findet man die Formel:
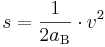 (s = Bremsweg in m, v = Geschwindigkeit in m/s und aB = Bremsbeschleunigung in m/s²).
(s = Bremsweg in m, v = Geschwindigkeit in m/s und aB = Bremsbeschleunigung in m/s²).
In dem folgenden GeoGebra-Applet kann der Bremsweg mit Hilfe der beiden Schieberegler oben links variiert werden.
Hinweis: Der Einfachheit halber wurde der obige Zusammenhang so verändert, dass die Geschwindigkeit in km/h angegeben wird.
|
Wie muss aB gewählt werden, damit ...
Nutze zur Lösung der Aufgabe das obere Applet. Um die Werte exakt einstellen zu können, klicke den Schieberegler an und verwende dann die Pfeiltasten.
|
In der Realität hängt der Wert der Bremsbeschleunigung aB von verschiedenen Faktoren ab. Im folgenden Video wird der Einfluss der Temperatur der Bremsen auf den Bremsweg untersucht. Der Pkw wird immer von einer Geschwindigkeit von 100 km/h bis zum Stillstand abgebremst und dabei der Bremsweg ermittelt.
|
|
Wenn wir die bisherigen Überlegungen verallgemeinern wollen, müssen wir unsere Gleichung für den Bremsweg genauer analysieren.
Zunächst stellen wir fest, dass es eine funktionale Abhängigkeit des Bremsweges von der Geschwindigkeit gibt; wir können unsere Formel als Funktionsgleichung schreiben:
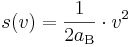 . Die rechte Seite der Funktionsgleichung besteht aus dem Vorfaktor
. Die rechte Seite der Funktionsgleichung besteht aus dem Vorfaktor 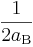 und dem Quadrat der Variablen.
und dem Quadrat der Variablen.
Besonders interessant ist dabei der Einfluss des Vorfaktors auf den Verlauf des Graphen:
|
Wie ändert sich der Verlauf des Graphen, wenn der Vorfaktor von v2, d.h. wenn
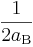 größer, wenn aB kleiner wird. Wenn aB kleiner wird, verläuft der Graph steiler. größer, wenn aB kleiner wird. Wenn aB kleiner wird, verläuft der Graph steiler. |
Merksatz: (Rein-)Quadratische Funktionen
Die Funktionen, die wir bis jetzt betrachtet haben, weisen eine Gemeinsamkeit auf: Ihr Funktionsterm hat die Form ax². Sie zählen daher zu den quadratischen Funktionen. Die Graphen quadratischer Funktionen unterscheiden sich stark von den Graphen linearer Funktionen.
|
Mit Hilfe des Schiebereglers (unten links im Applet) kannst du den Wert für a variieren. |

|
Als nächstes kannst du prüfen, ob du bis jetzt alles verstanden hast. |
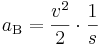
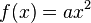 heißen Parabeln.
heißen Parabeln.
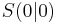 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
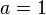 heißt der Graph Normalparabel.
heißt der Graph Normalparabel.

