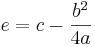Quadratische Funktionen 2 - quadratische Ergänzung: Unterschied zwischen den Versionen
| (15 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Durch quadratische Ergänzung bringst du einen Term <math> a x^2 + bx + c</math> auf die Form <math>a (x - d)^2 + e</math>. | + | {{Aufgabe|Durch quadratische Ergänzung bringst du einen Term <math> a x^2 + bx + c</math> auf die Form <math>a (x - d)^2 + e</math>. |
| − | + | <br> | |
| − | {{ | + | In dem Video wird erklärt wie man es macht. {{#ev:youtube |cDDxjzM0OX0|350}} }} |
| Zeile 7: | Zeile 7: | ||
# Klammere a aus: <math> a x^2 + bx + c = a (x^2 + \frac{b}{a} x + \frac{c}{a})</math> | # Klammere a aus: <math> a x^2 + bx + c = a (x^2 + \frac{b}{a} x + \frac{c}{a})</math> | ||
| − | # Ergänze <math> | + | # Ergänze in der Klammer <math> x^2 + \frac{b}{a} x </math> mittels der binomischen Formeln zu einem Quadrat, also <math> x^2 + \frac{b}{a} x = x^2 + \frac{2b}{2a} x = x^2 + \frac{2b}{2a} x + (\frac{b}{2a})^2 - (\frac{b}{2a})^2 = [x + (\frac{b}{2a})]^2 - (\frac{b}{2a})^2</math> |
| − | # Du hast also nun <math> a x^2 + bx + c = a [(x + (\frac{ | + | # Du hast also nun <math> a x^2 + bx + c = a [(x + (\frac{b}{2a}))^2 - (\frac{b}{2a})^2 + \frac{c}{a}] </math> |
| − | # Multipliziere die eckige Klammer aus und du erhältst: <math> a [(x + (\frac{ | + | # Multipliziere die eckige Klammer aus und du erhältst: <math> a [(x + (\frac{b}{2a}))^2 - (\frac{b}{2a})^2 + \frac{c}{a}] = a (x + (\frac{b}{2a}))^2 - \frac{b^2}{4a} + c</math> |
| − | Mit diesen 4 Schritten kannst du den Term <math> a x^2 + bx + c</math> auf die Form <math>a (x - d)^2 + e</math> bringen. Dabei ist <math> d = | + | Mit diesen 4 Schritten kannst du den Term <math> a x^2 + bx + c</math> auf die Form <math>a (x - d)^2 + e</math> bringen. Dabei ist <math> d = -\frac{b}{2a}</math> und <math>e = c - \frac{b^2}{4a}</math> |
}} | }} | ||
| + | |||
| + | Beispiele: | ||
| + | |||
| + | 1. Ergänze <math>x^2+6x</math> quadratisch.<br> | ||
| + | Schaue dir den Koeffizienten von x an: <span style="color:#C11111"> 6</span><br> | ||
| + | In der 1. binomischen Formel <math>x^2+2xa+a^2=(x+a)^2</math> ist beim mittleren Glied <math>2ax</math> bei <math>x</math> der Koeffizient 2. Also zerlege 6 in ein Produkt mit Faktor 2, also <math>6 = 2\cdot 3</math>.<br> | ||
| + | <math>x^2+6x=x^2+2\cdot 3x</math><br> | ||
| + | Ergänze nun mit der binomischen Formel <math>x^2+2xa+a^2=(x+a)^2</math> zu einem Quadrat, also <math>x^2+2\cdot 3 x +9=(x+3)^2</math>. <br> | ||
| + | Nun kann man nicht einfach <math>9</math> addieren, also subtrahiert man gleich wieder <math>9</math>.<br> | ||
| + | <math>f(x)=x^2+2\cdot 3x=x^2+2\cdot 3x + 9 - 9=(x+3)^2-9</math> | ||
| + | |||
| + | |||
| + | 2. Ergänze <math>x^2+6x+5</math> quadratisch.<br> | ||
| + | Schaue dir wieder den Koeffizienten von x an: <span style="color:#C11111"> 6</span><br> | ||
| + | In der 1. binomischen Formel <math>x^2+2xa+a^2=(x+a)^2</math> ist beim mittleren Glied <math>2ax</math> bei <math>x</math> der Koeffizient 2. Also zerlege 6 in ein Produkt mit Faktor 2, also <math>6 = 2\cdot 3</math>.<br> | ||
| + | <math>x^2+6x+5=x^2+2\cdot 3x +5</math><br> | ||
| + | Ergänze nun mit der binomischen Formel <math>x^2+2xa+a^2=(x+a)^2</math> zu einem Quadrat, also <math>x^2+2\cdot 3 x +9=(x+3)^2</math>. <br> | ||
| + | Nun kann man nicht einfach <math>9</math> addieren, also subtrahiert man gleich wieder <math>9</math>.<br> | ||
| + | <math>x^2+2\cdot 3x+5=x^2+2\cdot 3x + 9 - 9+5=(x+3)^2-9+5=(x+3)^2-4</math> | ||
| + | |||
| + | |||
| + | 3. Ergänze <math>x^2-6x+5</math> quadratisch <br> | ||
| + | Schaue dir wieder den Koeffizienten von x an: <span style="color:#C11111"> 6</span><br> | ||
| + | Nun steht vor dem mittleren Glied ein Minuszeichen. Daher verwende die 2. binomische Formel.<br> | ||
| + | In der 2. binomischen Formel <math>x^2-2xa+a^2=(x-a)^2</math> ist beim mittleren Glied <math>2ax</math> bei <math>x</math> der Koeffizient 2. Also zerlege 6 in ein Produkt mit Faktor 2, also <math>6 = 2\cdot 3</math>.<br> | ||
| + | <math>x^2-6x+5=x^2+2\cdot 3x+5</math><br> | ||
| + | Ergänze nun mit der binomischen Formel <math>x^2-2xa+a^2=(x-a)^2</math> zu einem Quadrat, also <math>x^2-2\cdot 3 x +9=(x-3)^2</math>. <br> | ||
| + | Nun kann man nicht einfach <math>9</math> addieren, also subtrahiert man gleich wieder <math>9</math>.<br> | ||
| + | <math>x^2-2\cdot 3x+5=x^2-2\cdot 3x + 9 - 9+5=(x-3)^2-9+5=(x-3)^2-4</math> | ||
| + | |||
| + | |||
| + | 4. Ergänze <math>2x^2-12x+10</math> quadratisch.<br> | ||
| + | Damit du das bisherige Verfahren anwenden kannst, klammere zuerst den Koeffizienten von <math>x^2</math> aus.<br> | ||
| + | <math>2x^2-12x+10=2(x^2-6x+5)</math><br> | ||
| + | In der Klammer steht nun der gleiche Term wie im Beispiel 3.<br> Gehe nun für den Klammerterm genauso vor wie in Beispiel 3, lass die <math>2</math> aber vor der Klammer stehen. Also ergibt sich:<br> | ||
| + | <math>2x^2-12x+10=2(x^2-6x+5)=2(x^2-2\cdot 3x + 5)=2(x^2+2\cdot 3x + 9 - 9 + 5)=2[(x-3)^2-9+5]=2[(x-3)^2-4]</math><br> | ||
| + | Löse nun die eckige Klammer auf <br> | ||
| + | <math>2x^2-12x+10=2[(x-3)^2-4]=2(x-3)^2-8</math> | ||
| + | |||
| + | |||
| + | 5. Ergänze <math>2x^2-10x-8</math> quadratisch.<br> | ||
| + | Gehe hier genauso wie im 4. Beispiel vor. Klammere zuerst den Koeffizienten von <math>x^2</math> aus. | ||
| + | <math>2x^2-10x-8=2(x^2-5x-4)</math><br> | ||
| + | Gehe nun für den Klammerterm genauso vor wie in Beispiel 3, lass die <math>2</math> aber vor der Klammer stehen. Also ergibt sich:<br> | ||
| + | <math>2x^2-10x-8=2(x^2-5x-4)=2(x^2-2\cdot 2,5x -4)=2(x^2+2\cdot 2,5x + 6,25 - 6,25 - 4)=2[(x-2,5)^2-6,25-4]=2[(x-2,5)^2-10,25]</math><br> | ||
| + | Löse nun die eckige Klammer auf <br> | ||
| + | <math>2x^2-10x-8=2[(x-2,5)^2-10.25]=2(x-2,5)^2-20,5</math> | ||
| + | |||
| + | |||
| + | Auf [https://www.mathebibel.de/quadratische-ergaenzung dieser Seite] ist das Verfahren der quadratischen Ergänzung auch nochmals erklärt. und auf dieser [http://www.willimann.org/A3110-Quadratische%20Funktionen%20-%20Uebung%202.pdf Seite] findest du Aufgaben. | ||
| − | + | ---- | |
| + | Zurück zu [[Quadratische_Funktionen_2_-_Allgemeine_quadratische_Funktion|'''Allgemeine quadratische Funktion''']] | ||
Aktuelle Version vom 9. Dezember 2020, 12:35 Uhr
|
Durch quadratische Ergänzung bringst du einen Term |
|
Mit diesen 4 Schritten kannst du den Term |
Beispiele:
1. Ergänze 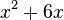 quadratisch.
quadratisch.
Schaue dir den Koeffizienten von x an: 6
In der 1. binomischen Formel 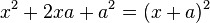 ist beim mittleren Glied
ist beim mittleren Glied 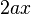 bei
bei  der Koeffizient 2. Also zerlege 6 in ein Produkt mit Faktor 2, also
der Koeffizient 2. Also zerlege 6 in ein Produkt mit Faktor 2, also 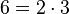 .
.
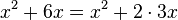
Ergänze nun mit der binomischen Formel 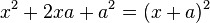 zu einem Quadrat, also
zu einem Quadrat, also  .
.
Nun kann man nicht einfach 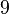 addieren, also subtrahiert man gleich wieder
addieren, also subtrahiert man gleich wieder 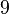 .
.
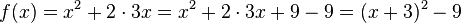
2. Ergänze 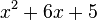 quadratisch.
quadratisch.
Schaue dir wieder den Koeffizienten von x an: 6
In der 1. binomischen Formel 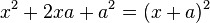 ist beim mittleren Glied
ist beim mittleren Glied 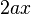 bei
bei  der Koeffizient 2. Also zerlege 6 in ein Produkt mit Faktor 2, also
der Koeffizient 2. Also zerlege 6 in ein Produkt mit Faktor 2, also 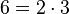 .
.
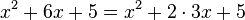
Ergänze nun mit der binomischen Formel 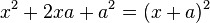 zu einem Quadrat, also
zu einem Quadrat, also  .
.
Nun kann man nicht einfach 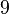 addieren, also subtrahiert man gleich wieder
addieren, also subtrahiert man gleich wieder 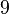 .
.
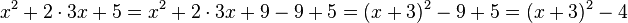
3. Ergänze 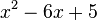 quadratisch
quadratisch
Schaue dir wieder den Koeffizienten von x an: 6
Nun steht vor dem mittleren Glied ein Minuszeichen. Daher verwende die 2. binomische Formel.
In der 2. binomischen Formel 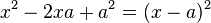 ist beim mittleren Glied
ist beim mittleren Glied 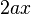 bei
bei  der Koeffizient 2. Also zerlege 6 in ein Produkt mit Faktor 2, also
der Koeffizient 2. Also zerlege 6 in ein Produkt mit Faktor 2, also 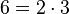 .
.
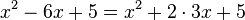
Ergänze nun mit der binomischen Formel 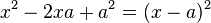 zu einem Quadrat, also
zu einem Quadrat, also 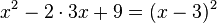 .
.
Nun kann man nicht einfach 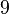 addieren, also subtrahiert man gleich wieder
addieren, also subtrahiert man gleich wieder 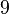 .
.
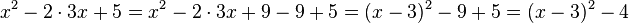
4. Ergänze  quadratisch.
quadratisch.
Damit du das bisherige Verfahren anwenden kannst, klammere zuerst den Koeffizienten von 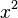 aus.
aus.
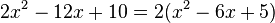
In der Klammer steht nun der gleiche Term wie im Beispiel 3.
Gehe nun für den Klammerterm genauso vor wie in Beispiel 3, lass die 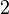 aber vor der Klammer stehen. Also ergibt sich:
aber vor der Klammer stehen. Also ergibt sich:
![2x^2-12x+10=2(x^2-6x+5)=2(x^2-2\cdot 3x + 5)=2(x^2+2\cdot 3x + 9 - 9 + 5)=2[(x-3)^2-9+5]=2[(x-3)^2-4]](/images/math/4/c/9/4c9bcd3acd417812b7fded58b8918052.png)
Löse nun die eckige Klammer auf
![2x^2-12x+10=2[(x-3)^2-4]=2(x-3)^2-8](/images/math/4/b/e/4bedd80de013a0cd39db4cd26cdaa4d4.png)
5. Ergänze 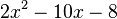 quadratisch.
quadratisch.
Gehe hier genauso wie im 4. Beispiel vor. Klammere zuerst den Koeffizienten von 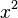 aus.
aus.
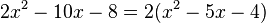
Gehe nun für den Klammerterm genauso vor wie in Beispiel 3, lass die 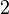 aber vor der Klammer stehen. Also ergibt sich:
aber vor der Klammer stehen. Also ergibt sich:
![2x^2-10x-8=2(x^2-5x-4)=2(x^2-2\cdot 2,5x -4)=2(x^2+2\cdot 2,5x + 6,25 - 6,25 - 4)=2[(x-2,5)^2-6,25-4]=2[(x-2,5)^2-10,25]](/images/math/6/f/8/6f8de945cafba492febf962179e39285.png)
Löse nun die eckige Klammer auf
![2x^2-10x-8=2[(x-2,5)^2-10.25]=2(x-2,5)^2-20,5](/images/math/a/a/7/aa7c225800ed88b6b8b60cb12fae1e9a.png)
Auf dieser Seite ist das Verfahren der quadratischen Ergänzung auch nochmals erklärt. und auf dieser Seite findest du Aufgaben.
Zurück zu Allgemeine quadratische Funktion
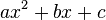 auf die Form
auf die Form 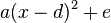 .
.
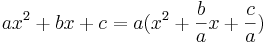
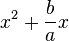 mittels der binomischen Formeln zu einem Quadrat, also
mittels der binomischen Formeln zu einem Quadrat, also ![x^2 + \frac{b}{a} x = x^2 + \frac{2b}{2a} x = x^2 + \frac{2b}{2a} x + (\frac{b}{2a})^2 - (\frac{b}{2a})^2 = [x + (\frac{b}{2a})]^2 - (\frac{b}{2a})^2](/images/math/3/d/7/3d7f8f652ef434bdb69d1fda79a33892.png)
![a x^2 + bx + c = a [(x + (\frac{b}{2a}))^2 - (\frac{b}{2a})^2 + \frac{c}{a}]](/images/math/a/9/0/a90fa95a547635e339d8e4ece3ee54d0.png)
![a [(x + (\frac{b}{2a}))^2 - (\frac{b}{2a})^2 + \frac{c}{a}] = a (x + (\frac{b}{2a}))^2 - \frac{b^2}{4a} + c](/images/math/c/0/8/c085313d761bdab2e67ef936ca1e6f42.png)
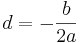 und
und