Rationale Funktionen Definitionen: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
so heißt die Funktion <math> f: \rightarrow f(x)</math> mit <math>f(x)= \frac{g(x)}{h(x)}</math> '''gebrochen-rationale Funktion'''. | so heißt die Funktion <math> f: \rightarrow f(x)</math> mit <math>f(x)= \frac{g(x)}{h(x)}</math> '''gebrochen-rationale Funktion'''. | ||
| + | |||
| + | Es ist <math>f(x) = \frac{a_zx^z+a_{z-1}x^{z-1}+ ... + a_1 x+a_0}{b_nx^n+b_{n-1}x^{n-1}+ ... + b_1 x+b_0}</math> mit <math>a_z, b_n\not=0</math> | ||
Die Definitionsmenge von <math>f</math> ist die Menge der reellen Zahlen ausgenommen die Nullstellen des Nennerpolynoms. | Die Definitionsmenge von <math>f</math> ist die Menge der reellen Zahlen ausgenommen die Nullstellen des Nennerpolynoms. | ||
Aktuelle Version vom 5. Februar 2013, 14:51 Uhr
|
Sind so heißt die Funktion Es ist Die Definitionsmenge von z ist der Grad des Zählerpolynoms, n der Grad des Nennerpolynoms. Ist z < n, dann ist |
Beispiel:
Die Funktion 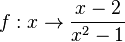 hat wegen
hat wegen 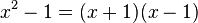 als Definitionsmenge
als Definitionsmenge 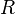 \ {-1;1}.
\ {-1;1}.
 ist eine echt gebrochen-rationale Funktion, da z=1 und n = 2, also z < n ist.
ist eine echt gebrochen-rationale Funktion, da z=1 und n = 2, also z < n ist.
|
Die Nullstellen des Nennerpolynoms werden als Definitionslücken bezeichnet. |
Beispiel:
Die Funktion 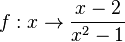 hat die Definitionslücken
hat die Definitionslücken 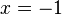 und
und 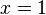 .
.
|
Ist an einer Definitionslücke
dann ist die Definitionslücke Die Gerade mit der Gleichung |
Beispiel:
Die Funktion 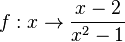 hat die Definitionslücken
hat die Definitionslücken 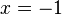 und
und 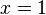 .
.
Es ist 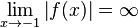 , da z(-1) = 1 ist.
, da z(-1) = 1 ist. 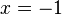 ist Polstelle und die Gerade
ist Polstelle und die Gerade 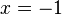 ist senkrechte Asymptote für den Graphen von f.
ist senkrechte Asymptote für den Graphen von f.
Ebenso ist 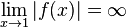 , da z(1) = 1 ist.
, da z(1) = 1 ist. 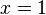 ist Polstelle und die Gerade
ist Polstelle und die Gerade 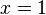 ist senkrechte Asymptote für den Graphen von f.
ist senkrechte Asymptote für den Graphen von f.
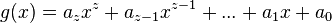 mit
mit 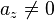 und
und 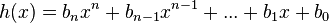 mit
mit 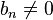 Polynome vom Grad z und n,
Polynome vom Grad z und n,
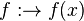 mit
mit 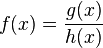 gebrochen-rationale Funktion.
gebrochen-rationale Funktion.
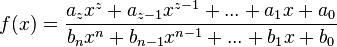 mit
mit 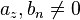
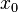 einer gebrochen-rationalen Funktion
einer gebrochen-rationalen Funktion 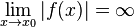 ,
,
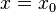 ist senkrechte Asymptote des Graphen von f.
ist senkrechte Asymptote des Graphen von f.

