Rationale Funktionen Einführung: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 21: | Zeile 21: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| − | 1. <center>[[Datei:Erde_tangenten-dreiecke.jpg | + | 1. <center>[[Datei:Erde_tangenten-dreiecke.jpg]]</center> |
In diesem Bild betrachet man die zwei rechtwinkligen Dreiecke <math>\Delta AMS</math> und <math> \Delta AMD</math>, welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich: | In diesem Bild betrachet man die zwei rechtwinkligen Dreiecke <math>\Delta AMS</math> und <math> \Delta AMD</math>, welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich: | ||
| Zeile 30: | Zeile 30: | ||
Formt man um <math> R-h = \frac{R^2}{R+x}</math> und löst nach h auf und fasst die rechte Seite zusammen, dann ergibt sich <math> h = R - \frac{R^2}{R+x}=\frac{R^2+Rx-R^2}{R+x}=\frac{Rh}{R+x}</math>. | Formt man um <math> R-h = \frac{R^2}{R+x}</math> und löst nach h auf und fasst die rechte Seite zusammen, dann ergibt sich <math> h = R - \frac{R^2}{R+x}=\frac{R^2+Rx-R^2}{R+x}=\frac{Rh}{R+x}</math>. | ||
| − | Setzt man den Term für h in die Formel für die Mantelfläche ein, so ergibt sich <math> M = \frac {2 \pi R^2 x}{R+x}</math> | + | Setzt man den Term für h in die Formel für die Mantelfläche ein, so ergibt sich <math> M = \frac {2 \pi R^2 x}{R+x}</math>. |
2. a) <math> D = [0;\infty[</math> | 2. a) <math> D = [0;\infty[</math> | ||
| Zeile 38: | Zeile 38: | ||
c) <math> M = 2 \pi R^2</math> | c) <math> M = 2 \pi R^2</math> | ||
}} | }} | ||
| + | |||
| + | |||
| + | |||
| + | Im Funktionsterm <math> \frac {2 \pi R^2 x}{R+x}</math> für <math>M</math> kommt die Variable x im Nenner des Bruches vor. Im Nenner steht ein linearer Term in x. <br> | ||
| + | Da der Nenner eines Bruches nie Null sein darf, muss man die Definitionsmenge beachten. <br> | ||
| + | Du hast so etwas schon bei der indirekten Proportionalität kennengelernt. Bei der Funktion <math> f: x \rightarrow \frac {1}{x}</math> darf auch <math>0</math> nicht eingesetzt werden.<br> | ||
| + | Man definiert allgemein solche Funktionen, bei denen x in einem Polynom im Nenner auftritt, als gebrochen-rationale Funktionen. | ||
| + | |||
| + | {{Merke|Sind <math>g(x) = a_zx^z+a_{z-1}x^{z-1}+ ... + a_1 x+a_0</math> mit <math>a_z\not=0</math> und <math>h(x) = b_nx^n+b_{n-1}x^{n-1}+ ... + b_1 x+b_0</math> mit <math>b_n\not=0</math> Polynome vom Grad <math>z</math> und <math>n</math> mit <math>z,n \in N</math>, | ||
| + | |||
| + | so heißt die Funktion <math> f: \rightarrow f(x)</math> mit <math>f(x)= \frac{g(x)}{h(x)}</math> '''gebrochen-rationale Funktion'''. | ||
| + | |||
| + | Es ist <math>f(x) = \frac{a_zx^z+a_{z-1}x^{z-1}+ ... + a_1 x+a_0}{b_nx^n+b_{n-1}x^{n-1}+ ... + b_1 x+b_0}</math> mit <math>a_z, b_n\not=0</math> | ||
| + | |||
| + | Die Definitionsmenge von <math>f</math> ist die Menge der reellen Zahlen ausgenommen die Nullstellen des Nennerpolynoms. | ||
| + | |||
| + | <math>z</math> ist der Grad des Zählerpolynoms, <math>n</math> der Grad des Nennerpolynoms. | ||
| + | |||
| + | Ist <math>z < n</math>, dann ist <math>f</math> eine '''echt''' gebrochen-rationale Funktion, ist <math>z \ge n</math>, dann ist <math>f</math> eine '''unecht''' gebrochen-rationale Funktion.}} | ||
| + | |||
| + | '''Beispiel:''' | ||
| + | |||
| + | Die Funktion <math>f:x\rightarrow \frac{x-2}{x^2-1}</math> hat wegen <math>x^2-1= (x+1)(x-1)</math> als Definitionsmenge <math>R</math>\ {-1;1}.<br> | ||
| + | <math>f</math> ist eine echt gebrochen-rationale Funktion, da <math>z=1</math> und <math>n = 2</math>, also <math>z < n</math> ist. | ||
| + | |||
| + | '''Bemerkung:''' | ||
| + | |||
| + | Unecht gebrochenrationale Funktion können mittels Polynomdivision in eine ganz-rationale Funktion und eine echt gebrochen-rationale Funktion aufgeteilt werden. | ||
| + | |||
| + | '''Beispiel für unecht gebrochen-rationale Funktionen:''' | ||
| + | |||
| + | 1. Für die Funktion <math>f:x\rightarrow \frac{x^2+2}{x^2-1}</math> ist der Funktionsterm umformbar. Es ist <math> | ||
| + | \frac{x^2+2}{x^2-1}=1+ \frac {3}{x^2-1}</math> | ||
| + | |||
| + | 2. Für die Funktion <math>f:x\rightarrow \frac{x^3+2}{x^2-1}</math> ist der Funktionsterm umformbar. Es ist <math> | ||
| + | \frac{x^3+2}{x^2-1}=x+ \frac {x+2}{x^2-1}</math> | ||
Aktuelle Version vom 25. März 2013, 14:33 Uhr
Astronauten, die von einer Raumstation,welche in der Höhe x um die Erde kreist, auf die Erde blicken, sehen eine Kugelhaube.
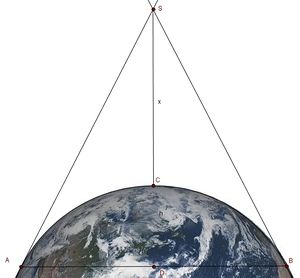
|
Die Mantelfläche 1. Zeige, dass die Mantelfläche Die Höhe 2. a) Bestimme die Definitionsmenge. b) Welchen Wert dürftest du nicht für x einsetzen? c) Welcher Grenzwert ergibt sich für die Mantelfläche
|
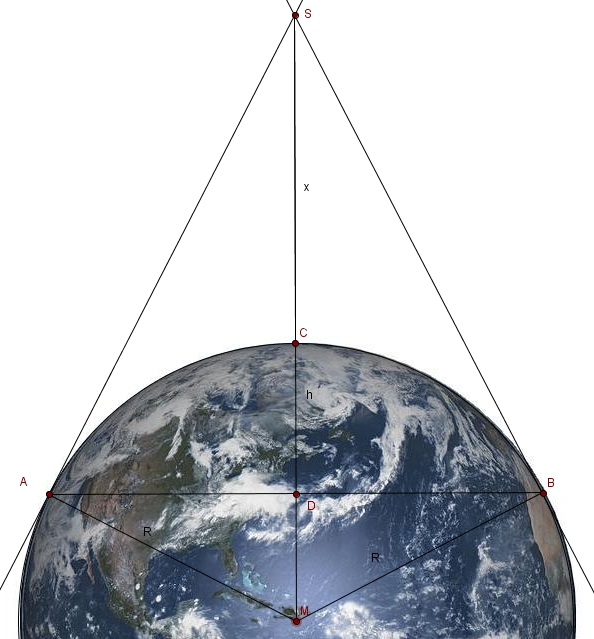
In diesem Bild betrachet man die zwei rechtwinkligen Dreiecke 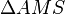 und
und 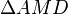 , welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich:
Im Dreieck
, welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich:
Im Dreieck 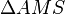 betrachtet man das Streckenverhältnis
betrachtet man das Streckenverhältnis 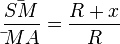 . Das entsprechende Seitenverhältnis im Dreieck
. Das entsprechende Seitenverhältnis im Dreieck 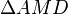 ist
ist 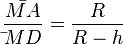 .
.
Also ist 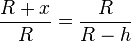 .
.
Formt man um 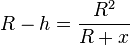 und löst nach h auf und fasst die rechte Seite zusammen, dann ergibt sich
und löst nach h auf und fasst die rechte Seite zusammen, dann ergibt sich 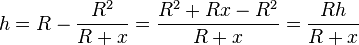 .
.
Setzt man den Term für h in die Formel für die Mantelfläche ein, so ergibt sich 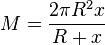 .
.
2. a) 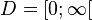
b) 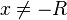
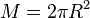
Im Funktionsterm 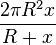 für
für 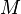 kommt die Variable x im Nenner des Bruches vor. Im Nenner steht ein linearer Term in x.
kommt die Variable x im Nenner des Bruches vor. Im Nenner steht ein linearer Term in x.
Da der Nenner eines Bruches nie Null sein darf, muss man die Definitionsmenge beachten.
Du hast so etwas schon bei der indirekten Proportionalität kennengelernt. Bei der Funktion 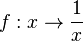 darf auch
darf auch 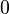 nicht eingesetzt werden.
nicht eingesetzt werden.
Man definiert allgemein solche Funktionen, bei denen x in einem Polynom im Nenner auftritt, als gebrochen-rationale Funktionen.
|
Sind so heißt die Funktion Es ist Die Definitionsmenge von
Ist |
Beispiel:
Die Funktion 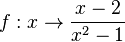 hat wegen
hat wegen 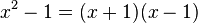 als Definitionsmenge
als Definitionsmenge 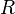 \ {-1;1}.
\ {-1;1}.
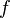 ist eine echt gebrochen-rationale Funktion, da
ist eine echt gebrochen-rationale Funktion, da 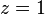 und
und 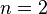 , also
, also 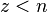 ist.
ist.
Bemerkung:
Unecht gebrochenrationale Funktion können mittels Polynomdivision in eine ganz-rationale Funktion und eine echt gebrochen-rationale Funktion aufgeteilt werden.
Beispiel für unecht gebrochen-rationale Funktionen:
1. Für die Funktion 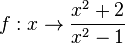 ist der Funktionsterm umformbar. Es ist
ist der Funktionsterm umformbar. Es ist 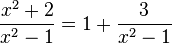
2. Für die Funktion 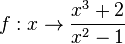 ist der Funktionsterm umformbar. Es ist
ist der Funktionsterm umformbar. Es ist 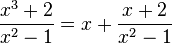
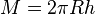 wobei
wobei 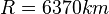 und
und 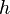 die Länge der Strecke [CD] ist.
die Länge der Strecke [CD] ist.
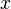 sich zu
sich zu 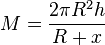 ergibt.
ergibt.
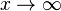 ?
?
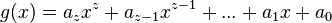 mit
mit 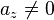 und
und 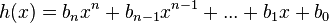 mit
mit 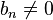 Polynome vom Grad
Polynome vom Grad 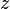 und
und 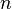 mit
mit 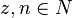 ,
,
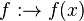 mit
mit 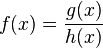 gebrochen-rationale Funktion.
gebrochen-rationale Funktion.
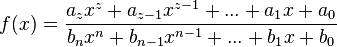 mit
mit 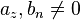
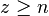 , dann ist
, dann ist 
