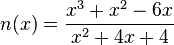Rationale Funktionen Nullstellen: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 46: | Zeile 46: | ||
f) <math>m</math> mit <math>m(x) = \frac{x^3+x^2-6x}{x^4+1}</math> | f) <math>m</math> mit <math>m(x) = \frac{x^3+x^2-6x}{x^4+1}</math> | ||
| − | g) <math> | + | g) <math>n</math> mit <math>n(x) = \frac{x^3+x^2-6x}{x^2+4x+4}</math> |
}} | }} | ||
Aktuelle Version vom 4. April 2013, 10:06 Uhr
Die Nullstellen einer gebrochen-rationalen Funktion findet man, indem man den Zähler der Funktion betrachtet, denn ein Bruch hat den Wert  , wenn der Zähler den Wert
, wenn der Zähler den Wert  hat.
hat.
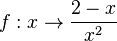 hat den Funktionswert
hat den Funktionswert  , wenn der Zähler
, wenn der Zähler 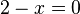 ist.
ist.
|
|
|
Ordne die Nullstellen und die angegebenen Funktionen |
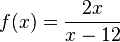 |

|
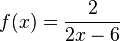 |
keine Nullstelle |
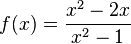 |
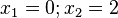
|
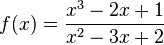 |
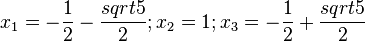
|
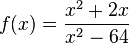 |
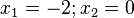
|
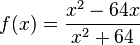 |
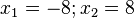
|
|
Ermittle jeweils die Nullstellen der Funktion: a) b) c) d) e) f) g) |
a) x = 13
b) x = -4 ; x = 4
c) keine
d) x = -2; x= -1
e) x= 2; x = 3
f) x = -3; x = 0; x = 2
g) x = -3; x = 0; (x = 2 muss näher untersucht werden, da 2 auch Nullstelle des Nenners ist!) mit
mit 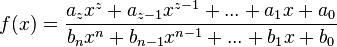 hat für
hat für 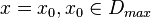 den Funktionswert Null, wenn das Zählerpolynom
den Funktionswert Null, wenn das Zählerpolynom 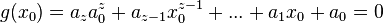 ist.
ist.
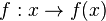 richtig zu!
richtig zu!
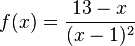
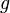 mit
mit 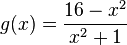
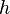 mit
mit 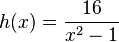
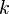 mit
mit 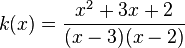
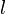 mit
mit 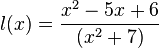
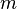 mit
mit 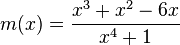
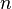 mit
mit