Trigonometrische Funktionen: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | {{ | + | {{Kasten1000| BREITE =100%| |
| − | + | ÜBERSCHRIFT =Informationen für den Lehrer| INHALT1=Hier sollen sich die Schüler mit der Variation von Parametern in Sinus- und Kosinusfunktionen beschäftigen und deren Auswirkungen erarbeiten und beschreiben können.| | |
| + | INHALT2=Ziele| INHALT2a='''Bekannt sind''' | ||
| − | + | *Darstellungsformen von Funktionen | |
| + | *Kenntnis der Auswirkung von Variationen in den Darstellungsformen von linearen und quadratischen Funktionen | ||
| + | *Eigenschaften der trigonometrischen Funktionen | INHALT2b='''Dabei lernt man''' | ||
| − | [[Trigonometrische Funktionen/Didaktischer Kommentar|Didaktischer Kommentar]] | + | *Erkennen der Auswirkung der Variation von Parametern im Funktionsterm auf die Graphen der Sinus- und Kosinusfunktion, und umgekehrt. |
| − | }} | + | *Unterschiedliche Variablenbezeichnungen identifizieren können | INHALT3=[[Trigonometrische Funktionen/Didaktischer Kommentar|Didaktischer Kommentar]]}} |
| − | |||
=== Hellsehen === | === Hellsehen === | ||
{| | {| | ||
Version vom 27. Dezember 2008, 10:23 Uhr
|
Informationen für den Lehrer
Hier sollen sich die Schüler mit der Variation von Parametern in Sinus- und Kosinusfunktionen beschäftigen und deren Auswirkungen erarbeiten und beschreiben können. Ziele
|
Inhaltsverzeichnis |
Hellsehen
| Wäre es nicht toll, wenn du hellsehen könntest? Wenn du den Graphen eines Funktionsterms auch ohne Wertetabelle direkt zeichnen könntest? Wenn du aus dem Graphen einer Funktion deren Term ablesen könntest?
Für die linearen und die quadratischen Funktionen beherrscht du diese Kunst wahrscheinlich schon. Dann wirst du vieles von Deinem Wissen auf die allgemeine Sinus- und Kosinusfunktion übertragen können. |
|
Einfluss der Parameter
Wiederholung:
Hefteintrag: Am besten verwendest du hierfür dein Heft im Querformat. Formuliere eine Überschrift und übernehme alle mit gelb gekennzeichneten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
|
Merke:
Die allgemeine Sinusfunktion lautet
Entsprechend lautet die allgemeine Kosinusfunktion
Dabei sind |
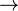 Hinweis: Bei den GeoGebra-Applets ist die
Hinweis: Bei den GeoGebra-Applets ist die 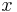 -Achse mit Vielfachen von
-Achse mit Vielfachen von 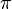 beschriftet. Indem man die
beschriftet. Indem man die 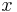 -Achse mit der rechten Maustaste anklickt und "Eigenschaften" wählt, kann man auf die Einheit cm umstellen.
-Achse mit der rechten Maustaste anklickt und "Eigenschaften" wählt, kann man auf die Einheit cm umstellen.
Arbeiten in Expertenteams
Einfluss von 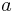 |
Einfluss von 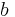 |
Einfluss von  |
Einfluss von 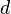
|
|---|---|---|---|
|
Untersuche hier den Einfluss von auf die Graphen der Funktionen und
|
Untersuche hier den Einfluss von auf die Graphen der Funktionen und
|
Untersuche hier den Einfluss von auf die Graphen der Funktionen und
|
Untersuche hier den Einfluss von auf die Graphen der Funktionen und
|
Arbeiten in Expertenteams
Sinus und Kosinus
|
Wie hängen die Sinus- und die Kosinusfunktion zusammen? Erstelle die Graphen
der Funktionen |
Lösung:
Ja genau, die Graphen der beiden Funktionen sind identisch. Genauer gesagt:
|
Merke:
Man erhält den Graphen der Kosinusfunktion indem man den Graphen der Sinusfunktion um Deshalb verhält sich die allgemeine Kosinusfunktion bei Variation ihrer Parameter genauso wie die allgemeine Sinusfunktion. |
Jetzt noch was zum Knobeln!!!
Du hast eine Menge über den Einfluss der einzelnen Parameter auf das Aussehen der Graphen heraus gefunden. Natürlich können aber die Parameter nicht nur einzeln variiert werden, sondern auch mehrere oder alle gleichzeitig.
|
Bestimmung einer Funktionsgleichung aus dem Graphen
Man kann dem Graphen einer Funktion ansehen, wie eine mögliche zugehörige Funktionsgleichung lautet. Öffne das folgende Applet und klicke in das leere Kontrollkästchen.
Anwendungen in der Physik
Wiederholung: Frequenz und Amplitude
|
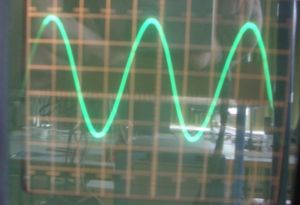
Auf einem Oszilloskop sieht man obiges Bild.
|
a) Die Sinuskurve ist um 0,75 nach oben verschoben.
Der Abstand zwischen Hoch- und Tiefpunkt der Sinuslinie ist 4,5, also ist die Amplitude 2,25.
Die Periodendauer ist 3,75.
Die Sinuskurve fängt mit 0,25 am linken Rand an.
b) Es sind d = 0,75, a = 2,25, b = 2*PI/3,75 und c = -0,224.
|
Super! Nun hast du es geschafft und das Ende des Lernpfades erreicht.
Hefteintrag: Lese dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alle gelb hinterlegten Texte übernommen hast.
Nun hast du es wirklich geschafft. Du kannst stolz sein - gut gemacht! Ich wünsche dir noch einen schönen Tag!
Zusatzaufgaben
|
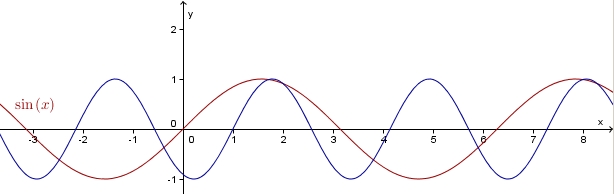
In dem unteren Bild sind der Graph der Sinusfunktion (rot) und ein weiterer Graph einer Sinusfunktion (schwarz) zu sehen.
|
a) Die Nullstellen der Sinusfunktion sind bei allen Vielfachen von PI, also x = k*PI.
b) Die Nullstellen der "schwarzen" Funktion sind bei x = 1, 1+PI/2, 1+PI, ...
c) Hochpunkte sind bei x = 1 + PI/4, 1 + 5/4*PI, ...
Tiefpunkte sind bei x = 1 - PI/4, 1 + 3/4*PI, ...
|

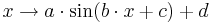
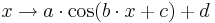
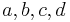 Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Im Folgenden seien
Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Im Folgenden seien 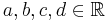 und
und 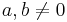 .
.
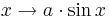
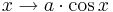 .
.
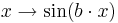
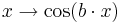 .
.
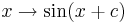
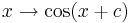 .
.
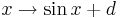
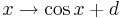 .
.
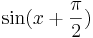 und
und 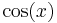 und
betrachte sie! Was fällt dir auf?
und
betrachte sie! Was fällt dir auf?
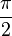 nach links verschiebt.
nach links verschiebt.
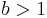 den Parameter
den Parameter 
