Anwendungen in der Physik: Unterschied zwischen den Versionen

Aus Medienvielfalt-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: ===Anwendungen in der Physik=== Wiederholung: [http://www.zum.de/dwu/pas002vs.htm Frequenz und Amplitude] 300px {{Arbeit|ARBEIT= Auf...)
 
Zeile 1: Zeile 1:
 +
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">
 +
[[Trigonometrische_Funktionen|Einführung]] - [[Trigonometrische Funktionen/Einfluss der Parameter|Einfluss der Parameter]] - [[Trigonometrische Funktionen/Bestimmung der Funktionsgleichung aus dem Graphen|Bestimmung der Funktionsgleichung aus dem Graphen]] - [[Trigonometrische Funktionen/Anwendungen in der Physik|Anwendungen in der Physik]] - [[Trigonometrische Funktionen/Zusatzaufgaben|Zusatzaufgaben]]
 +
</div>
 +
 +
 
===Anwendungen in der Physik===  
 
===Anwendungen in der Physik===  
 
Wiederholung: [http://www.zum.de/dwu/pas002vs.htm Frequenz und Amplitude]
 
Wiederholung: [http://www.zum.de/dwu/pas002vs.htm Frequenz und Amplitude]

Version vom 27. Dezember 2008, 16:57 Uhr

Einführung - Einfluss der Parameter - Bestimmung der Funktionsgleichung aus dem Graphen - Anwendungen in der Physik - Zusatzaufgaben


Anwendungen in der Physik

Wiederholung: Frequenz und Amplitude

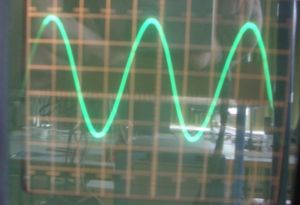
Oszilloskop.jpg
  Aufgabe   Stift.gif

Auf einem Oszilloskop sieht man obiges Bild.

  • Was kann man dort ablesen?
  • Wie erhält man aus dem Bild die nötigen Informationen?
  • Wie liest man aus der angezeigten Kurve Nullstellen, maximale Amplitude, Abstände, ... ab?

a) Die Sinuskurve ist um 0,75 nach oben verschoben.

Der Abstand zwischen Hoch- und Tiefpunkt der Sinuslinie ist 4,5, also ist die Amplitude 2,25.

Die Periodendauer ist 3,75.

Die Sinuskurve fängt mit 0,25 am linken Rand an.

b) Es sind d = 0,75, a = 2,25, b = 2*PI/3,75 und c = -0,224.
  Aufgabe   Stift.gif
  • In dem Applet auf dieser Seite wird gezeigt, wie man eine Schwingung darstellen kann. Mit dem Schieberegler für t kannst du die Schwingung darstellen. Überlege dir die gestellten Aufgaben und finde dann mit den angegebenen Größen y_max und T einen Funktionsterm für die zugehörige Sinusschwingung.
  • In dem Applet auf diesem Arbeitsblatt werden die Parameter einer Sinusschwingung aus der Physik behandelt. Welche Parameter a,b,c,d entsprechen welchen physikalischen Größen a, f, phi_0?
  • In diesem Lernpfad zur harmonischen Schwingung findest du als Lernschritt 8 eine Aufgabe. Kannst du sie lösen? Fertige eine Zeichnung an! Finde die entsprechenden Größen a,b,c,d von a sin(b x + c)+d?

Super! Nun hast du es geschafft und das Ende des Lernpfades erreicht.

Hefteintrag: Lese dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alle gelb hinterlegten Texte übernommen hast.

Nun hast du es wirklich geschafft. Du kannst stolz sein - gut gemacht! Ich wünsche dir noch einen schönen Tag!

Weiter geht es mit

Zusatzaufgaben

Von „http://medienvielfalt.zum.de/index.php?title=Trigonometrische_Funktionen/Anwendungen_in_der_Physik&oldid=1610“