Marie: Unterschied zwischen den Versionen
(→Aufgabe 1:) |
(→Aufgabe 1:) |
||
| Zeile 28: | Zeile 28: | ||
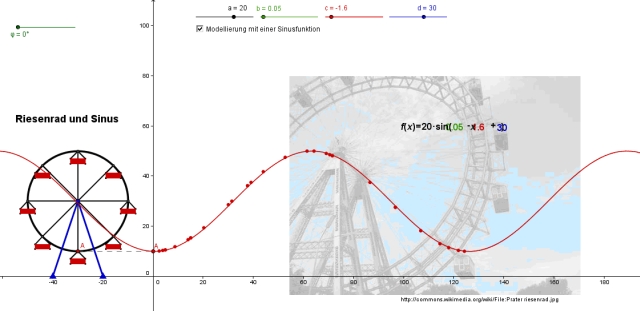
Die Sinusfunktion schaut im GeoGebra-Applet etwa so aus: | Die Sinusfunktion schaut im GeoGebra-Applet etwa so aus: | ||
[[Bild:Ggb-riesenrad-lsg.jpg]] | [[Bild:Ggb-riesenrad-lsg.jpg]] | ||
| − | :# Die Parameterwerte sind: a = 20, b = 0,05, c = -1, | + | :# Die Parameterwerte sind: a = 20, b = 0,05, c = -1,56, d = 30 |
| − | :# Die Sinusfunktion lautet: x --> 20sin(0,05x - 1, | + | :# Die Sinusfunktion lautet: x --> 20sin(0,05x - 1,56) + 30 |
}} | }} | ||
</div> | </div> | ||
Version vom 8. Januar 2011, 11:04 Uhr
Marie hat zwei Brieffreundinnen. Ines wohnt in Madrid, Maike in Hamburg. In den letzten Sommerferien treffen sich in Wien und gehen in den Prater. Dort bestaunen sie das Riesenrad. Maike fällt sofort als sie das Riesenrad sieht ein, dass sie im Mathematikunterricht die Sinusfunktion durch Abwickeln am Einheitskreis erhalten hat.
Tipp:
1. Falls du nicht mehr weißt wie das "Abwickeln am Einheitskreis" funktioniert, kannst du es hier nochmals anschauen.
2. Informationen zum Riesenrad im Wiener Prater findest du hier.
Maike meint nun, dass eine Gondel sicher auch eine Sinuslinie beschreibt. Marie und Ines möchten dies natürlich erklärt haben. Hilf ihnen, indem du folgendes GeoGebra-Applet öffnest:
Hinweis: Falls du nur ein leeres GeoGebra-Blatt mit Algebra-Ansicht und Zeichenblatt siehst, entferne die Algebra-Ansicht links, verkleinere das Blatt und verschiebe es so, dass du das Riesenrad, den Schieberegler, das Bild und den Funktionsterm auf deinem Bildschirm sehen kannst. So sollte dein Bildschirm aussehen: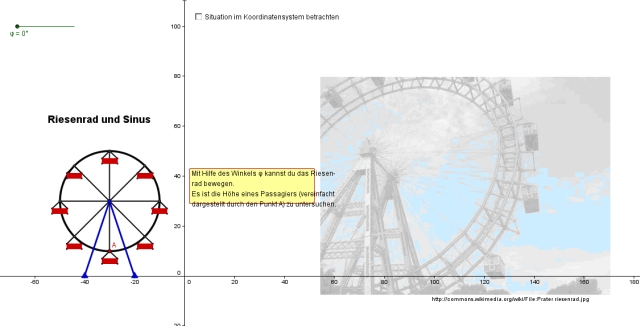 
Aufgabe 1:
a) Verändere nun den Winkel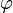 
mit dem Schieberegler.
b) Klicke an „Situation im Koordinatensystem betrachten“ – Drehe dabei das Riesenrad ganz langsam.
c) Bringe den Schieberegler für den Drehwinkel 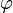auf 0° und klicke „Modellierung mit einer Sinusfunktion“ an.
d) Erzeuge mit Hilfe der Schieberegler für a, b, c und d eine Sinuskurve, auf der die Punkte des Riesenrads liegen.
e) Lies die Parameterwerte für a, b, c und d ab. Notiere die Sinusfunktion.
Die Sinusfunktion schaut im GeoGebra-Applet etwa so aus:
- Die Parameterwerte sind: a = 20, b = 0,05, c = -1,56, d = 30
- Die Sinusfunktion lautet: x --> 20sin(0,05x - 1,56) + 30
