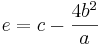Quadratische Funktionen 2 - quadratische Ergänzung: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(Die Seite wurde neu angelegt: „Durch quadratische Ergänzung bringst du einen Term <math> a x^2 + bx + c</math> auf die Form <math>a (x - d)^2 + c</math>. Wie du das machst wird dir [http://hom…“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | Durch quadratische Ergänzung bringst du einen Term <math> a x^2 + bx + c</math> auf die Form <math>a (x - d)^2 + | + | Durch quadratische Ergänzung bringst du einen Term <math> a x^2 + bx + c</math> auf die Form <math>a (x - d)^2 + e</math>. Wie du das machst wird dir [http://home.fonline.de/fo0126//algebra/alg4.htm hier] erklärt. |
| + | |||
| + | {{Merke| | ||
| + | |||
| + | # Klammere a aus: <math> a x^2 + bx + c = a (x^2 + \frac{b}{a} x + \frac{c}{a})</math> | ||
| + | # Ergänze <math> (x^2 + \frac{b}{a} x </math> mittels der binomischen Formeln zu einem Quadrat, also <math> (x^2 + \frac{b}{a} x = x^2 + \frac{2b}{2a} x = x^2 + \frac{2b}{2a} x + (\frac{2b}{a})^2 - (\frac{2b}{a})^2 = [x + (\frac{2b}{a})]^2 - (\frac{2b}{a})^2</math> | ||
| + | # Du hast also nun <math> a x^2 + bx + c = a [(x + (\frac{2b}{a}))^2 - (\frac{2b}{a})^2 + \frac{c}{a}] </math> | ||
| + | # Multipliziere die eckige Klammer aus und du erhältst: <math> a [(x + (\frac{2b}{a}))^2 - (\frac{2b}{a})^2 + \frac{c}{a}] = a (x + (\frac{2b}{a}))^2 - \frac{4b^2}{a} + c]</math> | ||
| + | |||
| + | Mit diesen 4 Schritten kannst du den Term <math> a x^2 + bx + c</math> auf die Form <math>a (x - d)^2 + e</math> bringen. Dabei ist <math> d = (\frac{2b}{a}))^2</math> und <math>e = c - \frac{4b^2}{a}</math> | ||
| + | }} | ||
Auf dieser [http://www.willimann.org/A3110-Quadratische%20Funktionen%20-%20Uebung%202.pdf Seite] findest du Aufgaben und die [http://www.willimann.org/A3110-Quadratische%20Funktionen%20-%20Uebung%202.pdf Lösungen] dazu. | Auf dieser [http://www.willimann.org/A3110-Quadratische%20Funktionen%20-%20Uebung%202.pdf Seite] findest du Aufgaben und die [http://www.willimann.org/A3110-Quadratische%20Funktionen%20-%20Uebung%202.pdf Lösungen] dazu. | ||
Version vom 6. Juli 2011, 17:58 Uhr
Durch quadratische Ergänzung bringst du einen Term 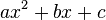 auf die Form
auf die Form 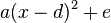 . Wie du das machst wird dir hier erklärt.
. Wie du das machst wird dir hier erklärt.
|
Mit diesen 4 Schritten kannst du den Term |
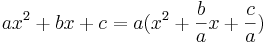
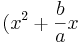 mittels der binomischen Formeln zu einem Quadrat, also
mittels der binomischen Formeln zu einem Quadrat, also ![(x^2 + \frac{b}{a} x = x^2 + \frac{2b}{2a} x = x^2 + \frac{2b}{2a} x + (\frac{2b}{a})^2 - (\frac{2b}{a})^2 = [x + (\frac{2b}{a})]^2 - (\frac{2b}{a})^2](/images/math/e/2/1/e21f80917d7ae29432dfa66098733bcd.png)
![a x^2 + bx + c = a [(x + (\frac{2b}{a}))^2 - (\frac{2b}{a})^2 + \frac{c}{a}]](/images/math/7/e/e/7ee446e4b1fd9287a555d6a141941153.png)
![a [(x + (\frac{2b}{a}))^2 - (\frac{2b}{a})^2 + \frac{c}{a}] = a (x + (\frac{2b}{a}))^2 - \frac{4b^2}{a} + c]](/images/math/c/2/4/c24d1ca36df12ae1876ddf0808f9a8c2.png)
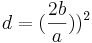 und
und