Symmetrie: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 2: | Zeile 2: | ||
---- | ---- | ||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=1| | ||
| + | ARBEIT= Schau dir diesen Video an: | ||
| + | |||
| + | {{#ev:youtube |KF22N-l9OOE|350}} | ||
| + | |||
| + | |||
| + | Schreibe eine Definition Achsensymmetrie zur y-Achse bzw. für Punktsymmetrie zum Ursprung eines Funktionsgraphen auf. | ||
| + | |||
| + | }} | ||
| + | |||
| + | {{Merksatz|MERK= | ||
| + | * Der Graph einer Funktion f ist achsensymmetrisch zur y-Achse, wenn <math>f(-x) = f(x)</math> ist. Die Funktion <math>f</math> heißt '''gerade'''. | ||
| + | * Der Graph einer Funktion f ist punktsymmetrisch zum Ursprung des Koordinatensystems, wenn <math>f(-x) = - f(x)</math> ist. Die Funktion <math>f</math> heißt '''ungerade'''. | ||
| + | }} | ||
| + | |||
| + | Im folgenden Video siehst du Beispiele zur Symmetrie: | ||
| + | |||
| + | <center>>{{#ev:youtube |gL3ea3Nbz_Y|350}}</center> | ||
| − | |||
---- | ---- | ||
zurück zu [[Funktionen_Einstieg/Eigenschaften von Funktionen|Eigenschaften von Funktionen]] | zurück zu [[Funktionen_Einstieg/Eigenschaften von Funktionen|Eigenschaften von Funktionen]] | ||
Version vom 3. Januar 2012, 17:43 Uhr
zurück zu Eigenschaften von Funktionen
|
Schau dir diesen Video an:
|
|
Merke:
|
Im folgenden Video siehst du Beispiele zur Symmetrie:
zurück zu Eigenschaften von Funktionen

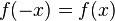 ist. Die Funktion
ist. Die Funktion  heißt gerade.
heißt gerade.
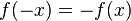 ist. Die Funktion
ist. Die Funktion 
