|
|
| Zeile 8: |
Zeile 8: |
| | Man weiß von einem Würfel, dass es das Volumen 27 VE hat. Wie lang ist dann die Seite? Natürlich 3 LE. | | Man weiß von einem Würfel, dass es das Volumen 27 VE hat. Wie lang ist dann die Seite? Natürlich 3 LE. |
| | | | |
| − | Es ist | + | Es ist |
| | + | |
| | + | <center><math> a = V^{\frac{1}{3}}</math></center> |
| | + | |
| | + | Man schreibt auch dafür |
| | + | |
| | <center><math> a = \sqrt[3]{V}\</math></center> | | <center><math> a = \sqrt[3]{V}\</math></center> |
| | | | |
| Zeile 17: |
Zeile 22: |
| | | | |
| | | | |
| − | {{Aufgabe|a) Setze verschiedene Werte für V ein, und berechne welche Werte | + | {{Merksatz|MERK= |
| − | sich für a ergeben. Trage die Ergebnisse in eine Wertetabelle ein. | + | Die Gleichung <math> a = x^n</math> hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung<br> |
| | + | <center> <math> x = a^{\frac{1}{n}}</math> oder <math> x = \sqrt[n]{a}\</math></center> |
| | + | |
| | + | <math> \sqrt[n]{a}\</math> heißt die''' n-te Wurzel aus a'''. |
| | + | }} |
| | + | |
| | + | |
| | + | |
| | + | {{Aufgabe|a) Setze verschiedene Werte für das Würfelvolumen V ein, und berechne welche Werte |
| | + | sich für die Seitenlänge a ergeben. Trage die Ergebnisse in eine Wertetabelle ein. |
| | | | |
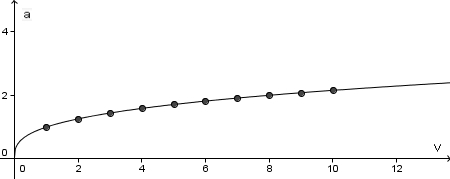
| | b) Erstelle ein V-a-Diagramm (V nach rechts, a nach oben antragen!)}} | | b) Erstelle ein V-a-Diagramm (V nach rechts, a nach oben antragen!)}} |
| Zeile 29: |
Zeile 43: |
| | [[Datei:Wuerfel_V-a-graph_2.jpg]] }} | | [[Datei:Wuerfel_V-a-graph_2.jpg]] }} |
| | | | |
| − | Mit dem folgenden Applet wird über dem Volumen V, welches du mit dem Schieberegler variieren kannst, die Seitenlänge a aufgetragen. Du siehst außerdem wie sich der Würfel dabei ändert.
| + | |
| − | <ggb_applet width="792" height="472" version="4.0" ggbBase64="UEsDBBQACAAIAI+QPUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAI+QPUAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vptb9s2EP7c/QpCn7YhtklRL1bhdGiSpinQrQXSFcM+DKAkWmatt0my4xT98TuSkizHdlI1TeFkRVuK5JHHe56748n25LdVEqMlL0qRpccGGWID8TTIQpFGx8aimg7Gxm8vfppEPIu4XzA0zYqEVceGJSVFeGy4PvYwDcMBcTEdWHQcDBinZBD6tkN826M8sA2EVqV4nmZ/sISXOQv4ZTDjCXubBaxSimdVlT8fja6uroaNqmFWRKMo8oerMjQQHDMtj4364Tlst7HoiipxE2My+uv3t3r7gUjLiqUBN5A0YSFe/PRsciXSMLtCVyKsZsfGGIMZMy6iGdjkyM5ICuUASM6DSix5CUs7XWVzleSGEmOpnH+mn1DcmmOgUCxFyItjAw9NsD8rBE+repbUWkbN+slS8Cu9kXxSOiwDVVkW+0zugb58QSY2MTqSDdGNCY3j6CmsxzDVjakbSze2lrH0ckuLWlrG0jIWNdBSlMKP+bExZXEJmIl0WgBfbb+srmOuzlMPrO0lR2BTKT6DMJUgapBhHOMj+Q+QPbIadDtGko7Wqlj0VNqodD3z61Wa9zKUNjrNXWaa9h4znVuUaru/xk5id3SCKvVX/dvSSG8z86ZG3b+fQsf6ISZORk2oTOroQOVMytbeU/GklPFCPWR70u0JsiE2HBe83EbEg8Y1EUQDIjaybOiSMXJk6yLqwoSFKBojKUcoUsFhj+E/y1WbOciGzeSoCzGJCCiykE0RUTFlIYgkpOISYtSkIGHbyIZFUj0x5RbUQZYDPTpGFpxRhqRLQJDCQuiDehNRgqhcTFxkOsiR+xFLhrozlkeHLU3kYOQQuSFENUS0jmaQHyMqrXFquESaL6oNiIIkbB6rLG+5AGnIR+s8p/PTRhp8NomZz2O4GS4lkwgtWSwjQimaZmmFGhJNPRYVLJ+JoLzkVQWrSvSJLdlbVvHVOUiXjW4lG2Rp+b7IqtMsXiRpiVCQxbg9cxaTzrPZnho6tDNhdSfszoTTeXZ36s1gBi1KDvqzomzEWRi+kRLr1ABIvkvj65OCs3meiU0zJiN1yUz4IohFKFj6EZxVapG4oObOUemquXMsy2oOkhXh5XUJHoxWf/MiA//35CV7rTt0bA297h8IuDJgMtwsb3NmDOxf75nztDa+bElhK97aGxUi7D6/KU+yOGytVwafsrxaFKo+gGxYSDNeplHMlVOo/AqXbzD3s9Wl9gaq9/pwnUMPa/1+pIBGkAxMG+7HqG593SoZebBWCisZrCRw414ibOeJBDWqW1+3Sgr8VR+tNpQ0VhLcqBGlSmHY2AgU5ezyKl+konrbdCoRzGtLiZb/Y5H4fO0yUuBM6LpDF1SbWsjDaZmMbjjeZM6LlMe1nwPdi2xR6rDthEDIA5FAV0/UsDFJ6Z9wJj0a8qjgtTyLVX2mQVWzuOvCW8Nqq/MiS96kyw/gLzcOMBk1p5yUQSFy6ZXIh7thzteeF4qSwdUSdtfJwAQ0AnmFACCVRAtCdlHNskKVYJBpoJXxGPMEyi9UKRdMFwkvRNBi/1HVcnCoRX1ub1iDIIFHmf8JUuANvlRHycD0HidFLM5nTFaApHZFds2LDWjUbr9nYa24litjWTqiRKRqm4StZFkF+/klZMcKimfgIl0Xz/pkdXaBwkRmDVjiqhr9Gta68mEqVh1AASPxGXyCbRizDpYKEvccqtNSRXRVx656uBBhyNP2tCwF71EcQO7KtbkIrg2unb1dmoP5Kmt0mK+J2aJIJZoW7JfG7WR0fHkfGyq5tHzgr+QD97CQ7LKwjolS0oFrNlT7uZMalLEyV25cqHr0RjBtILbKC+BHHqvG4RTe3VZwvp8//vMzQSNEfzlC7eMvxia2oztAP/020GUdGOnG1823or5Gzhxiz6auR7BDLWp6lq2A3DX8ILieNbjie+B5djh4Np74wwB81QI4tNGvqOOeNwb6gvrqcEAF1CzXGXu2TYlLHMs1Fca7hh8E4/MGY/KdMT4/HIzpkFgUO2PH9mxieRZxfyzGr/diTO6H8euDx3jX8INgfLE3V9wT44vDwXhPrvhhGJ/sKBRwXzxPDgfPPQXC96q0gixJWBqiVH2YdckjOW6sP15hWNaoiBEJijZ4UTUTTO9W77GFaVnv1qDG7kC134vH7Yi+m05LXkkAB7S+rchOwEnPCmKt+BveJ/i/qV5S6hdgkeSxCETVIhvLIvtNWsHrMFcvf9uvtHPOc/l5w7v0Q8HSUn5poWUa+PrSe6LpPd2i1+9Hr3//V5mv5/eWiBncETLWkHrYIdT2PIoxNukT4/NU83m2xWfQj8/gQPhsAnInr/8DPs80ny+3+Az78RkeCJ93hOeTTbDnWwTyfgTyAyFw0O990BwS4Bs7ruc5NsaE2E+M33PN7+stfqf9+J0eCr93RKgztMe2Z2LqAdcY06fG5+t9BVHUj8/oQPjcE647w/hJJuCLfRXRrB+hs8dJ6JNPwBf7ErDox684EH7veAUdPPUEXF+or7b4/NSPz08Hxue+N5ibAbr19f4uPiGKHw2hr/a9wsz7ETo/EEIf5kZ9TIy+3Helxv0YjQ+E0btq3qdXFNUxebHFYNKPweSRMPiok+z29xzv2+857vHF/ftv+kT+O3zNsfWpu/xd0gN+bz/q/qBK/Zix/iX+i/8AUEsHCFtbylnRBwAAJjAAAFBLAQIUABQACAAIAI+QPUDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAj5A9QFtbylnRBwAAJjAAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABoCAAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | + | |
| | + | {{Merksatz|MERK= |
| | + | Man definiert für jede natürliche Zahl n die allgemeine Wurzelfunktion n-ten Grades oder n-te Wurzelfunktion |
| | + | |
| | + | <math> f: x \rightarrow \sqrt[n]{x}\</math> mit <math> x \in R^+_0</math> und <math>n \in N</math>. |
| | + | }} |
Version vom 30. Januar 2012, 08:41 Uhr
Ein Würfel mit Seitenlänge a hat dasVolumen 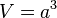 .
.
Man weiß von einem Würfel, dass es das Volumen 27 VE hat. Wie lang ist dann die Seite? Natürlich 3 LE.
Es ist
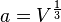
Man schreibt auch dafür
Fehler beim Parsen(Lexikalischer Fehler): a = \sqrt[3]{V}\
|
Merke:
Die Gleichung 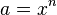 hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung
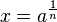 oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\ oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\
Fehler beim Parsen(Lexikalischer Fehler): \sqrt[n]{a}\
heißt die n-te Wurzel aus a.
|
 Aufgabe Aufgabe
a) Setze verschiedene Werte für das Würfelvolumen V ein, und berechne welche Werte
sich für die Seitenlänge a ergeben. Trage die Ergebnisse in eine Wertetabelle ein.
b) Erstelle ein V-a-Diagramm (V nach rechts, a nach oben antragen!)
|
[Lösung anzeigen][Lösung ausblenden]
|
Merke:
Man definiert für jede natürliche Zahl n die allgemeine Wurzelfunktion n-ten Grades oder n-te Wurzelfunktion
Fehler beim Parsen(Lexikalischer Fehler): f: x \rightarrow \sqrt[n]{x}\
mit  und und 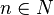 . .
|
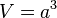 .
.
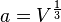
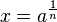 oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\
oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\


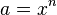 hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung
hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung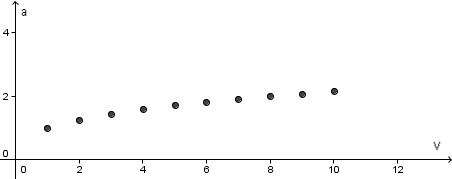
 und
und 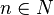 .
.

