Wurzelfunktion allgemeine Wurzelfunktion: Unterschied zwischen den Versionen
| Zeile 58: | Zeile 58: | ||
<math>f:V \rightarrow \sqrt[3]{V}</math> mit <math>V \in R^+_0</math> | <math>f:V \rightarrow \sqrt[3]{V}</math> mit <math>V \in R^+_0</math> | ||
}} | }} | ||
| + | |||
| + | |||
{{Arbeiten|NUMMER=2| | {{Arbeiten|NUMMER=2| | ||
| Zeile 66: | Zeile 68: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | + | 1. Stelle mit dem Schieberegler die passende Wurzelfunktion ein. | |
<ggb_applet width="713" height="271" version="4.0" ggbBase64="UEsDBBQACAAIAFB2P0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACABQdj9AAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbL1XW2/bNhR+bn/FgZ42oLFFipLswmmxbigWIO0GpBuGPQygJdpmI5GCSPlS9MfvkJRkOb0gW7EFTUiKH/mdO09XL491BXvRGqnVdURmcQRCFbqUansddXZztYhevni62gq9FeuWw0a3NbfXEXNIWeKRNGcsp8kVy5fFFSs4u+IiL682JKc8oVwsKI8AjkY+V/otr4VpeCHuip2o+a0uuPXEO2ub5/P54XCYDVQz3W7n2+16djRlBCimMtdRP3mO110cOiQeTuOYzP94cxuuv5LKWK4KEYFToZMvnj5ZHaQq9QEOsrS76yinJIKdkNsd6pQslxHMHahBgzSisHIvDB6dLL3Otm4iD+PK7T8JM6hGdSIo5V6Wor2O4hnN82RJUxKzmFKyJEkEupVC2R5MetL5cN1qL8Uh3OtmnpJFYLWu1txdCR8/Ao1pDM/cQMJAcciysBWHb3ESBhoGFoY0YFg4zgKUBQwLGIYy7qWR60pcRxteGTShVJsW3TeujT1VwsvTfzirT56hTkZ+QHASY5wEm+P3OH7mfjP8ZW5jfqkkmbDatvuHpANl7iz8WEr6TYomAyf9nJo0/YKa2VdIg96P0ZOkE06k8v/87yeMydfUfMgY1t9GmLH/RcXVfEiVVZ8dYHYO20ePFbVx+ZIsIV26sCeQYm5kOUZ5CmSJQ04BswFICizFJVlA5sYckhw3GCSwAIcjCfjkSBf4h+X+sgxSvMx9zTEngSARgzQB4nOKAWYS+LzEHKUJItIUUjzk6Al1VyQZsAxXyQIYyuhSMicITPAgrpGeQkIgcYdJDjSDzN1HmEv1bOFExyspZDFkxF2IWY0ZHbIZ8QtInDZZby6pms5emKioy2FqdTP6AtFYj85lL9Sni6r4ZFXxtajwobhzngTY88plhCfaaGVhcCIN37Ytb3ayMHfCWjxl4D3f81tuxfE1os3A7bGFVubXVtsfddXVygAUuopHmXVFJnM6So2LZLLBphvpZCObzPPP8mrcgc4I5NetGeC8LG8c4lwa0JK/qOr0qhX8vtHyUo3V3L85K9EVlSwlV79jsDoWZxcYnyBXroYniLJkEES35d3JYATD8U/RarQji2fL6Q/m2ClsYcWexdMfV5gK7pKPLS8PLfDQl7aywC32o4v4UYzab1tZTuc35pWuytEWXv0feWO71jcPKELrlPpBbSvhQ8RXW3yZi/u1Pt6F2EjCXe9ODa7iwL/eerMDlgaapgjox3UYPcYJNqJij4k9Ih6CTZbjPllSj/DjOowehdEbROsVJYOWJB5opPEFLY4u0saHvnvnOyXt7bCwsrjvNSUB/7ar1+IcQA7wkwxNSei2LlnIf8eymj8Iw9W9aJWo+qhHd3e6MyGJJwlRikLWuAwbvdm4c+lvKFP4WoptK3o8r3zzFozqd+NpQH/y2V/1utX1jdq/w3h5IMBqPki5MkUrGxeVsMaX4l6cI6+UhuNDU07PuTRFaxTuQUGDWGctTODO7nTr+zOsOzi67KxEjc0YWB+CqqtFK4vR9so3eihU18tNB6c5w4Nev8eC+MBffuExuP2FIAVeNTvu2kPShyI/ifbCNP62N7rsiXucqVxfCbUM72TNjz5aga8N1kqLnTX6Qp076yBZX2uwK3F9+9H1ZW5ycq+qm2zkcWJQtJH8gDHBL5Q5J4vFMn6PvarxGW373PWTn2VZCjVKyxVGj/cBVrImBGwjRAj18WCDyvuaMfF77xbvyrrmqgTlm4fXnfJOjc7vGceX4fjXdwTmoL5HS5BgYHwXbtRGYpieem90doBvAkl/9SdRsBlIBpduoq+7fJIxj/F5/Eifx//W8lP7zae54F+l/n9YL/4GUEsHCN7WoqhsBQAA/g0AAFBLAQIUABQACAAIAFB2P0BFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAUHY/QN7WoqhsBQAA/g0AAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAAEBgAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="713" height="271" version="4.0" ggbBase64="UEsDBBQACAAIAFB2P0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACABQdj9AAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbL1XW2/bNhR+bn/FgZ42oLFFipLswmmxbigWIO0GpBuGPQygJdpmI5GCSPlS9MfvkJRkOb0gW7EFTUiKH/mdO09XL491BXvRGqnVdURmcQRCFbqUansddXZztYhevni62gq9FeuWw0a3NbfXEXNIWeKRNGcsp8kVy5fFFSs4u+IiL682JKc8oVwsKI8AjkY+V/otr4VpeCHuip2o+a0uuPXEO2ub5/P54XCYDVQz3W7n2+16djRlBCimMtdRP3mO110cOiQeTuOYzP94cxuuv5LKWK4KEYFToZMvnj5ZHaQq9QEOsrS76yinJIKdkNsd6pQslxHMHahBgzSisHIvDB6dLL3Otm4iD+PK7T8JM6hGdSIo5V6Wor2O4hnN82RJUxKzmFKyJEkEupVC2R5MetL5cN1qL8Uh3OtmnpJFYLWu1txdCR8/Ao1pDM/cQMJAcciysBWHb3ESBhoGFoY0YFg4zgKUBQwLGIYy7qWR60pcRxteGTShVJsW3TeujT1VwsvTfzirT56hTkZ+QHASY5wEm+P3OH7mfjP8ZW5jfqkkmbDatvuHpANl7iz8WEr6TYomAyf9nJo0/YKa2VdIg96P0ZOkE06k8v/87yeMydfUfMgY1t9GmLH/RcXVfEiVVZ8dYHYO20ePFbVx+ZIsIV26sCeQYm5kOUZ5CmSJQ04BswFICizFJVlA5sYckhw3GCSwAIcjCfjkSBf4h+X+sgxSvMx9zTEngSARgzQB4nOKAWYS+LzEHKUJItIUUjzk6Al1VyQZsAxXyQIYyuhSMicITPAgrpGeQkIgcYdJDjSDzN1HmEv1bOFExyspZDFkxF2IWY0ZHbIZ8QtInDZZby6pms5emKioy2FqdTP6AtFYj85lL9Sni6r4ZFXxtajwobhzngTY88plhCfaaGVhcCIN37Ytb3ayMHfCWjxl4D3f81tuxfE1os3A7bGFVubXVtsfddXVygAUuopHmXVFJnM6So2LZLLBphvpZCObzPPP8mrcgc4I5NetGeC8LG8c4lwa0JK/qOr0qhX8vtHyUo3V3L85K9EVlSwlV79jsDoWZxcYnyBXroYniLJkEES35d3JYATD8U/RarQji2fL6Q/m2ClsYcWexdMfV5gK7pKPLS8PLfDQl7aywC32o4v4UYzab1tZTuc35pWuytEWXv0feWO71jcPKELrlPpBbSvhQ8RXW3yZi/u1Pt6F2EjCXe9ODa7iwL/eerMDlgaapgjox3UYPcYJNqJij4k9Ih6CTZbjPllSj/DjOowehdEbROsVJYOWJB5opPEFLY4u0saHvnvnOyXt7bCwsrjvNSUB/7ar1+IcQA7wkwxNSei2LlnIf8eymj8Iw9W9aJWo+qhHd3e6MyGJJwlRikLWuAwbvdm4c+lvKFP4WoptK3o8r3zzFozqd+NpQH/y2V/1utX1jdq/w3h5IMBqPki5MkUrGxeVsMaX4l6cI6+UhuNDU07PuTRFaxTuQUGDWGctTODO7nTr+zOsOzi67KxEjc0YWB+CqqtFK4vR9so3eihU18tNB6c5w4Nev8eC+MBffuExuP2FIAVeNTvu2kPShyI/ifbCNP62N7rsiXucqVxfCbUM72TNjz5aga8N1kqLnTX6Qp076yBZX2uwK3F9+9H1ZW5ycq+qm2zkcWJQtJH8gDHBL5Q5J4vFMn6PvarxGW373PWTn2VZCjVKyxVGj/cBVrImBGwjRAj18WCDyvuaMfF77xbvyrrmqgTlm4fXnfJOjc7vGceX4fjXdwTmoL5HS5BgYHwXbtRGYpieem90doBvAkl/9SdRsBlIBpduoq+7fJIxj/F5/Eifx//W8lP7zae54F+l/n9YL/4GUEsHCN7WoqhsBQAA/g0AAFBLAQIUABQACAAIAFB2P0BFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAUHY/QN7WoqhsBQAA/g0AAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAAEBgAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| − | + | 2. (0;0 und (1;1) | |
| + | }} | ||
| + | |||
| + | |||
| + | {{Arbeiten|NUMMER=3| | ||
| + | ARBEIT= | ||
| + | Betrachte nun die Wurzelfunktionen im folgenden Applet: | ||
| + | <ggb_applet width="792" height="370" version="4.0" ggbBase64="UEsDBBQACAAIAMV2P0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACADFdj9AAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbL1XWY/bNhB+Tn7FQE8JkLVFnXYgJ2hSBF1gkxbYtCj6UICSaJlZiRREypaD/PgMScmWNwe2DVpjvTxmyG9ujrOXQ1PDnnWKS7HxyML3gIlCllxUG6/X26uV9/LF46xismJ5R2Eru4bqjRcZTl7ikTiNojQIr6J0XVxFBY2uKEvLqy1JAxoGlK0C6gEMij8X8h1tmGppwW6LHWvojSyotsA7rdvny+XhcFhMUAvZVcuqyheDKj1AMYXaeOPkOV53cegQWvbA98nyz7c37vorLpSmomAeGBV6/uLxo+zARSkPcOCl3m28lY9q7Bivdkan9cqDpWFq0SAtKzTfM4VHZ0urs25az7JRYeiP3AzqkzoelHzPS9ZtPH8RxB7IjjOhRyoZUZbT+WzP2cFdZGYWI/JAS1nn1NwBnz5B4Ac+PDMDcUOAQ5I4ku/2/NANgRsiN8SOJ3LHI8caOZ7I8UShB3uueF6zjbeltUKbcbHt0F+ntdLHmll5xo2zvuQZ6qT4R2QOjUWdkXHf95+Zb4LfyBCWl0qSGaru+n8IOkGm6+DhkMEPKRpOmMHX1Azib6iZfAfU6f0QPUk8w0Qo+2e/XyCG31PzPqJb/xhgEv0vKmbLKVWyMTtA7QzvGD2aNcrkS7iGeG3CnkCMuZGkGOUxkDUOaQCYDUBiiGJckhUkZkwhTJEQQQgrMHwkBJsc8Qr/Ram9LIEYLzO7KeYkEASKIA6B2JyKADMJbF5ijgYhcsQxxHjIwJPAXBEmECW4ClcQoYwmJVOCjCEexDXCBxASCM1hkkKQQGLuI5FJ9WRlRMcrA0h8SIi5ELMaM9plM/KvIDTaJKO5uGh7fWGioimnqZbtyRfIjfXoXOdcfboog4+ymuasxpfh1ngSYE9rkxEWaCuFhsmJgdurOtrueKFumdZ4SsEHuqc3VLPhDXKrCdvyFlKo3zqpX8u6b4QCKGTtn2SWNZnNg5PUuAhnhGhOiGeEZDZPv4orkQK9YogvOzWx07K8Nhzn0oCW/FXUx1cdo3et5JdqZEv7yGSsL2pecir+wGA1KMYuML05tlxNb04YBZMgsitvjwojGIa/WCexxqSrhT//oFePjkRW5JJkClNBTfJF68V6/sE37TiSYv/+IQvN9icP0YGdlK86Xs7n1+qVrMuTKaz2r2mr+842CyhBZ3T6SVQ1sxFiiy2+xMVdLodbFxqhu+v9scWV7/DzylodsDIEMT6W1TjmbrQ8RrATl295fMvhT7HGyxOdGAtX45i70XJh8DrRRkXJpCXxJxiubD3zvYussZFv3vVecH0zLTQv7kZNieN/1zc5O8ePYfiZuybEdVeXKOS/Q8mW96Iwu2OdYPUY9OjuXvbK5fAsH0pW8AaXjjCajRqX/o4yud2SVR0b+WltmzVnVEv15/H8xba96k0nm2uxf4/xck+AbDlJmami462JSsjxobhj58gruaL4zpTzcyZL0RqFeU/QINpYC/O31zvZ2X4Myw6OJjlr1mAvBtqGoOgb1vHiZHthGzsUqh/lDianGcODzD9gPbznL7uwPEj+RpACrdsdNe0gGUORHll3YRp721tZjsAjn6pNHwkNd89kQwcbrUBzhaVSYyeNvhDnTtpJNpYabEpMnz6YtsxMjq4GeLDlw8ygaCP+EWOCXihzThaNVfwOW1VlM1qPuWsnv/CyZOIkLRUYPdYHWMhaF7AtYy7UTwdbVN7WjJnfR7cYBw1th1jmktHAW/xRMpi36snwFDYw/P2EwBLEU/dsXTp02wsbBN758Pe9Nwv+h7jPf6D7/H9rxLkplvOwtu/L+OPoxWdQSwcIetFQyVAFAAC5DQAAUEsBAhQAFAAIAAgAxXY/QEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACADFdj9AetFQyVAFAAC5DQAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAOgFAAAAAA==" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | # Was ist der Unterschied zu Aufgabe 2? | ||
| + | # Wieso | ||
}} | }} | ||
Version vom 31. Januar 2012, 14:55 Uhr
Ein Würfel mit Seitenlänge a hat dasVolumen 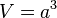 .
.
Man weiß von einem Würfel, dass es das Volumen 27 VE hat. Wie lang ist dann die Seite? Natürlich 3 LE.
Es ist
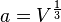
Man schreibt auch dafür
|
Merke:
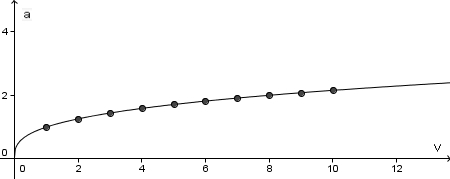
Die Gleichung 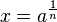 oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\ oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\
Fehler beim Parsen(Lexikalischer Fehler): \sqrt[n]{a}\ heißt die n-te Wurzel aus a. |
|
a) Setze verschiedene Werte für das Würfelvolumen V ein, und berechne welche Werte sich für die Seitenlänge a ergeben. Trage die Ergebnisse in eine Wertetabelle ein. b) Erstelle ein V-a-Diagramm (V nach rechts, a nach oben antragen!) |
|
Merke:
Man definiert für jede natürliche Zahl n die allgemeine Wurzelfunktion n-ten Grades oder n-te Wurzelfunktion Fehler beim Parsen(Lexikalischer Fehler): f: x \rightarrow \sqrt[n]{x}\ mit |
|
Gib für die Würfelaufgabe die zugehörige Funktion an. |
![f:V \rightarrow \sqrt[3]{V}](/images/math/5/6/2/56277ceb06d9f1e85ce77b321e54ee46.png) mit
mit 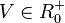
|
1. Stelle mit dem Schieberegler die passende Wurzelfunktion ein.
2. (0;0 und (1;1)
|
Betrachte nun die Wurzelfunktionen im folgenden Applet:
|


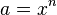 hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung
hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung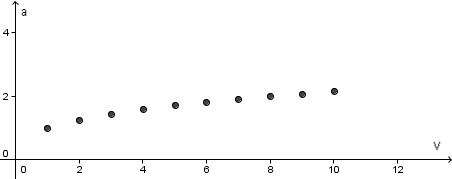
 und
und 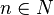 .
.

