Einfluss von d: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 13: | Zeile 13: | ||
{{Arbeiten|NUMMER=D1|ARBEIT= | {{Arbeiten|NUMMER=D1|ARBEIT= | ||
| − | <ggb_applet height=" | + | <ggb_applet height="350" width="400" type="button" filename="sin_d.ggb" /> <br> |
# Öffne dieses GeoGebra-Applet. Mit dem Schieberegler kannst du den Wert von <math> \ d </math> ändern. <br> | # Öffne dieses GeoGebra-Applet. Mit dem Schieberegler kannst du den Wert von <math> \ d </math> ändern. <br> | ||
| Zeile 69: | Zeile 69: | ||
{{Arbeiten|NUMMER=D4|ARBEIT= | {{Arbeiten|NUMMER=D4|ARBEIT= | ||
| − | <ggb_applet height=" | + | <ggb_applet height="350" width="400" type="button" filename="Cos_d.ggb" /> <br> |
Öffne dieses GeoGebra-Applet und bearbeite damit die Aufgabe D1 noch einmal <math>cos</math>. | Öffne dieses GeoGebra-Applet und bearbeite damit die Aufgabe D1 noch einmal <math>cos</math>. | ||
Aktuelle Version vom 23. November 2016, 08:36 Uhr
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Einfluss von d
|
Wir betrachten nun den Einfluss von
|
|
|
|
Nun betrachten wir den Einfluss von
|
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe D1 ein Hefteintrag "versteckt" ist!
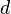 in
in
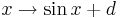 .
.
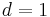 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 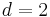 und
und 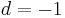 sowie
sowie 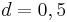 auf den Graphen auswirken und überprüfe deine Vermutung.
auf den Graphen auswirken und überprüfe deine Vermutung. 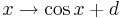 .
.
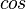 .
.

