Rationale Funktionen Definitionen: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(Die Seite wurde neu angelegt: „{{Merke|Sind <math>g(x) = a_zx^z+a_{z-1}x^{z-1}+ ... + a_1 x+a_0</math> mit <math>a_z\not=0</math> und <math>h(x) = b_nx^n+b_{n-1}x^{n-1}+ ... + b_1 x+b_0</math> …“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | {{Merke|Sind <math>g(x) = a_zx^z+a_{z-1}x^{z-1}+ ... + a_1 x+a_0</math> mit <math>a_z\not=0</math> und <math>h(x) = b_nx^n+b_{n-1}x^{n-1}+ ... + b_1 x+b_0</math> mit <math> | + | {{Merke|Sind <math>g(x) = a_zx^z+a_{z-1}x^{z-1}+ ... + a_1 x+a_0</math> mit <math>a_z\not=0</math> und <math>h(x) = b_nx^n+b_{n-1}x^{n-1}+ ... + b_1 x+b_0</math> mit <math>b_n\not=0</math> Polynome vom Grad z und n, |
so heißt die Funktion <math> f: \rightarrow f(x)</math> mit <math>f(x)= \frac{g(x)}{h(x)}</math> '''gebrochen-rationale Funktion'''. | so heißt die Funktion <math> f: \rightarrow f(x)</math> mit <math>f(x)= \frac{g(x)}{h(x)}</math> '''gebrochen-rationale Funktion'''. | ||
Version vom 31. Januar 2013, 15:11 Uhr
|
Sind so heißt die Funktion Die Definitionsmenge von z ist der Grad des Zählerpolynoms, n der Grad des Nennerpolynoms. Ist z < n, dann ist |
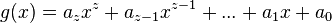 mit
mit 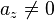 und
und 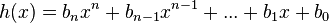 mit
mit 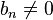 Polynome vom Grad z und n,
Polynome vom Grad z und n,
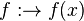 mit
mit 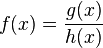 gebrochen-rationale Funktion.
gebrochen-rationale Funktion.
 ist die Menge der reellen Zahlen ausgenommen die Nullstellen des Nennerpolynoms.
ist die Menge der reellen Zahlen ausgenommen die Nullstellen des Nennerpolynoms.

