Rationale Funktionen Nullstellen: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 1: | Zeile 1: | ||
| − | Die Nullstellen einer gebrochen-rationalen Funktion findet man, indem man den Zähler der Funktion betrachtet. | + | Die Nullstellen einer gebrochen-rationalen Funktion findet man, indem man den Zähler der Funktion betrachtet, denn ein Bruch hat den Wert <math>0</math>, wenn der Zähler den Wert <math>0</math> hat. |
<math>f:x \rightarrow \frac{2-x}{x^2}</math> hat den Funktionswert <math>0</math>, wenn der Zähler <math> 2-x = 0</math> ist. | <math>f:x \rightarrow \frac{2-x}{x^2}</math> hat den Funktionswert <math>0</math>, wenn der Zähler <math> 2-x = 0</math> ist. | ||
Version vom 27. Februar 2013, 15:05 Uhr
Die Nullstellen einer gebrochen-rationalen Funktion findet man, indem man den Zähler der Funktion betrachtet, denn ein Bruch hat den Wert  , wenn der Zähler den Wert
, wenn der Zähler den Wert  hat.
hat.
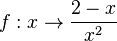 hat den Funktionswert
hat den Funktionswert  , wenn der Zähler
, wenn der Zähler 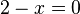 ist.
ist.
|
|
|
Ordne die Nullstellen und die angegebenen Funktionen |
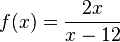 |

|
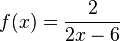 |
keine Nullstelle |
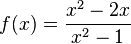 |
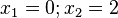
|
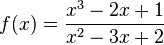 |
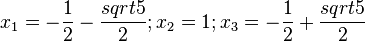
|
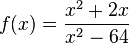 |
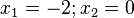
|
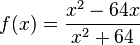 |
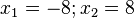
|
 mit
mit 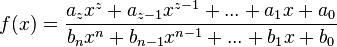 hat für
hat für 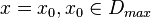 den Funktionswert Null, wenn das Zählerpolynom
den Funktionswert Null, wenn das Zählerpolynom 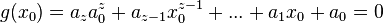 ist.
ist.
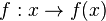 richtig zu!
richtig zu!

