Rationale Funktionen Indirekte Proportionalitaet: Unterschied zwischen den Versionen

Aus Medienvielfalt-Wiki
Wechseln zu: Navigation, Suche
Zeile 3: Zeile 3:
 
x bezeichne die Anzahl der Kinder und y die Anzahl der Schokoladenstückchen, die jedes Kind bekommt. <br>
 
x bezeichne die Anzahl der Kinder und y die Anzahl der Schokoladenstückchen, die jedes Kind bekommt. <br>
  
−
<div style="margin:0;  border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1F1FF; align:left;">
+
{{Arbeiten|NUMMER=1|
−
'''Aufgabe:''' Vervollständige die Tabelle:  
+
ARBEIT=
−
{| class="wikitable"
+
a) Vervollständige die Tabelle: http://wikis.zum.de/rsg/images/6/67/Tab-24-x.jpg
−
! x || 1 || 2 || 3 || 4  || 6 || 8 || 12 || 24
+
−
|-
+
−
| y ||  ||    ||    ||  ||  ||  ||    ||
+
−
|-
+
−
|}
+
−
</div>
+
  
−
{{Lösung versteckt|
+
b) Zeichne den Graph für dieses Beispiel.
−
 
+
−
http://wikis.zum.de/rsg/images/3/31/Tab-24-x-lsg.jpg
+
 
}}
 
}}
−
 
−
<div style="margin:0;  border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1F1FF; align:left;">
 
−
'''Aufgabe:''' Zeichne den Graph für dieses Beispiel.<br>
 
−
</div>
 
  
 
{{Lösung versteckt|
 
{{Lösung versteckt|
  
−
http://wikis.zum.de/rsg/images/b/bc/24-x.jpg
+
a) http://wikis.zum.de/rsg/images/3/31/Tab-24-x-lsg.jpg
 +
 
 +
b) http://wikis.zum.de/rsg/images/b/bc/24-x.jpg
 
}}
 
}}
  
 
Betrachte die Produkte x*y, so stellst du fest, dass x*y= 24 ist.
 
Betrachte die Produkte x*y, so stellst du fest, dass x*y= 24 ist.
  
−
<div style="margin:0;  border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1E1FF; align:left;">
+
{{Merke|
−
Eine Zuordnung zwischen zwei Größen x und y heißt '''indirekt proportional''', wenn das Produkt x*y für alle Paare (x,y) stets konstant ist. </div>
+
 
 +
Eine Zuordnung zwischen zwei Größen x und y heißt '''indirekt proportional''', wenn das Produkt x*y für alle Paare (x,y) stets konstant ist.  
 +
}}
  
  
−
In diesem Beispiel kann x nur eine natürliche Zahl zwischen 1 und 24 sein.  
+
In diesem Beispiel ist x eine natürliche Zahl zwischen 1 und 24.  
  
 
Man kann die Funktion http://wikis.zum.de/rsg/images/0/05/F24-x.jpg allgemein für alle rationalen Zahlen x, die ungleich Null sind, erklären. <br>
 
Man kann die Funktion http://wikis.zum.de/rsg/images/0/05/F24-x.jpg allgemein für alle rationalen Zahlen x, die ungleich Null sind, erklären. <br>
 
Der Graph dieser Funktion schaut dann so aus: <br>
 
Der Graph dieser Funktion schaut dann so aus: <br>
−
</center>http://wikis.zum.de/rsg/images/6/64/F24-x-graph.jpg</center><br>
+
<center>http://wikis.zum.de/rsg/images/6/64/F24-x-graph.jpg</center><br>
  
 
<center>Der Graph einer indirekten Proportionalität heißt '''Hyperbel'''.</center>
 
<center>Der Graph einer indirekten Proportionalität heißt '''Hyperbel'''.</center>
  
  
−
<div style="margin:0;  border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1E1FF; align:left;">
+
{{Merke|
 
Die Funktion http://wikis.zum.de/rsg/images/a/a6/Fm_x_term.jpg mit einer rationalen Zahl m heißt '''indirekte Proportionalität''' oder indirekt proportionale Funktion.  
 
Die Funktion http://wikis.zum.de/rsg/images/a/a6/Fm_x_term.jpg mit einer rationalen Zahl m heißt '''indirekte Proportionalität''' oder indirekt proportionale Funktion.  
−
</div>
+
}}
  
−
Was ist Definitionsmenge, Wertemenge? Ist der Graph symmetrisch?<br>
+
{{Arbeiten|NUMMER =2|
 +
ARBEIT=
 +
Bestimme die Definitionsmenge und die Wertemenge.
  
−
{{Lösung versteckt|
+
Ist der Graph symmetrisch bezüglich des Koordinatensystems?
 +
}}
 +
 
 +
{{Lösung versteckt|1=
 
Da x im Nenner steht, darf x nicht 0 sein, also ist die Definitionsmenge <math>R</math>\{<math>0</math>}.<br>
 
Da x im Nenner steht, darf x nicht 0 sein, also ist die Definitionsmenge <math>R</math>\{<math>0</math>}.<br>
 
<div style="margin:0;  border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1E1FF; align:left;">
 
<div style="margin:0;  border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1E1FF; align:left;">
 
Eine solche Stelle, an der der Funktionsterm nicht definiert ist und in deren Nähe die Funktionswerte nach + Unendlich oder - Unendlich gehen, heißt '''Polstelle'''.
 
Eine solche Stelle, an der der Funktionsterm nicht definiert ist und in deren Nähe die Funktionswerte nach + Unendlich oder - Unendlich gehen, heißt '''Polstelle'''.
 
</div>
 
</div>
−
</center>http://wikis.zum.de/rsg/images/6/64/F24-x-graph.jpg</center><br>
+
<center>http://wikis.zum.de/rsg/images/6/64/F24-x-graph.jpg</center><br>
  
 
Aus dem Graph sieht man, dass 0 als Funktionswert nicht angenommen wird, ansonsten kommen alle reelle Zahlen als y-Werte vor, also ist die Wertemenge auch <math>R</math>\{<math>0</math>}.
 
Aus dem Graph sieht man, dass 0 als Funktionswert nicht angenommen wird, ansonsten kommen alle reelle Zahlen als y-Werte vor, also ist die Wertemenge auch <math>R</math>\{<math>0</math>}.
  
 
Desweiteren sieht man, dass der Graph punktsymmetrisch zum Ursprung ist.
 
Desweiteren sieht man, dass der Graph punktsymmetrisch zum Ursprung ist.
−
 
 
}}
 
}}
  
−
 
+
{{Arbeiten|NUMMER = 3|
−
 
+
ARBEIT=
−
<div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1F1FF; align:left;">
+
a) Stelle in diesem Applet
−
'''Aufgaben:'''<br>
+
<ggb_applet width="604" height="484" version="4.2" ggbBase64="UEsDBBQACAAIAFyAhkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFyAhkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVjbjts2EH3efMVATy3gtUXdbAd2giRF0QCbNOimRdE3SqJtZiVREClfgnx8Z0jJlp1ksc2mMeKlSQ05c84MD6ksnu/LArai0VJVS4+NfQ9ElalcVuul15rV9cx7/uzJYi3UWqQNh5VqSm6WXjQOvNM87I1ZTJNlvvT8eSpCJqbX/iwPrqNZHl/Pwyi8XoXRbJWnPMjTyAPYa/m0Um95KXTNM3GbbUTJb1TGjV1zY0z9dDLZ7Xbj3vtYNevJep2O9zr3ACOv9NLrfjzF5c4m7UJrHvg+m/z95sYtfy0rbXiVCQ8IVSufPbla7GSVqx3sZG42Sy9hiGwj5HqDMOMQI52QUY1Ya5EZuRUapw66FrMpa8+a8YqeX7lfUBzheJDLrcxFg/yMg2Q6n4azOAn8OYv90APVSFGZzpZ1Pif9aoutFDu3LP2yHjEwo1SRcloR4jl8+gSBH/gwooa5JsAmSdwj3435oWsC10SuiZ1N5KZHzjRyNpGziTDMrdQyLcTSW/FCI4myWjWYwGNfm0MhbEjdwIkANkJYWn5EY/TngWMdYx/5o8i3Xwd7gHE2wMgIwCdgFLltQqCYmY2dmqjrJq47tQ3zu9EZ/bEkJY+EEfYwwiEMXH1E3+QrUNjAq2na/+i0d5n40cOYCx4F8giRJRf+gq/Bu49Vh/ch+HAznPzF/sj+s9/PPIb3Qbz06PqPc0hU/FiIkT+ffneQWLWj0I9GSfRlp1P/TFh6VXEt69ofwv1i0sveogsI9IZsu/1jRKkpxHBu5Q8YxCgRyRTVKgY2x2ZKUhEAiyGKsctmkFA7hZDUIYIQZkB2LAQrcvEM/0RWORKIcS0anPpWSSCMIA6BWWmMAFkAK6/ISRCiRRxDjJPIOyO3YQJRgp1wBhEGSMI6JQELcR720XkAIYOQ5rIpBAkkAUxJnFlEmp3MKHZcNIDEh4SmojqjMjtVxhkzCAkN7rxaaenI9ensKupjViyPsqpb03HXjWdl3vNo1IV5rrK7l0eyuyeCazM0w8PpdAS6w+rshLxaFDwVBd4jbqkSALa8IGGxHlaqMtBXQeDG1g2vNzLTt8IYnKXhA9/yG27E/le01r1v69oe3AvRZoXMJa/+wjKhJWhBOJ7jJJX9OR5hVVsvmVJNfnvQWDuw/0c0ijZEMI6HH5x36B6x+Xg++OB5pDNORR8E42D4waI+fPkRm3egxfYIje+F7ulfN7TrOmKp81q/VMVpqFayMq94bdrGXspQmxsC9aJaF8Jya9UerzfZXar2t47U0K31/lALKgobQLp+pQrVAO7JII7RoGtT11obiuxo5Vsb31r4fZZkfnzO5oG1sG3qWmuFaXehdUhZD5P5vRup3V3RO9vTtmbostRW0tz0HSOzuw4pc/Zv2zLFcjuWMBr8It3NDsGML72w/8/LYnJRhos70VSicMVWYb5b1WpX/ccKvlq0WrzjZvOiyv8Qa9y57ziJp0FvztR6dLtRZLLEiW68I5hT8v/E6N1oLtaN6Ox5Ye/Kjn779Kz0Pxu2S/3aqPJ1tX2PlXUR6mLS41norJE1FTCkqOZ34lSjudQcz4J8OA/Ba0SRkS4hdYZ49YC3ZqMaex3GrY27FF7UjSxQTbFkaU8XosSLMBhbuFVbikZmx4yV9o6NAbYdBtanmtIFKv2A+nOR5ROT+PgrpQ28qDecbuasK2B+EM0ZTXa1NyrvHXduC7rSQylReq9xK5V8T4KCC6ZaFa3BtxpMTHV6q3GhdRKFRzG9M+EU++50QJ2yb2AruR+Qi3zJj1hJ52Vx2mIGVfMO3xO01QHT7Xj74zeZ56I6RssrrCSbD9S/2pV5LYTbIMeJNYK3SjOogS4tlKB93aAvWqQjeFXi6bCnM6T8af8zLKGECezdIXGezlVb2XLwBlO/Z/L8e5P3+2qlhSG2p4klO0i+mNrPNGxAcHgfwffRBAi2p8mxxCxLDyHpmzgK6Ph7FEv0vnewR8k9LF2WFO2ghxXVt5TwkOHJUGDspaD7X4Jn/wJQSwcIWq7vW+cFAADVEAAAUEsBAhQAFAAIAAgAXICGQtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACABcgIZCWq7vW+cFAADVEAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAH4GAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
−
1. Stelle in dieser [http://www.rsg.rothenburg.de/wiki/images/4/47/Aufg_24-x-n.ggb GeoGebra-Datei] den Schieberegler für m so ein, dass es den Graphen von [[bild:f24-x.jpg|center]] zeigt.<br>
+
den Schieberegler für m so ein, dass es den Graphen von http://wikis.zum.de/rsg/images/6/64/F24-x-graph.jpg zeigt.<br>
 
2. Beantworte die Fragen auf dieser [http://www.realmath.de/Neues/Klasse8/hyperbel/hyperbel.html Seite]
 
2. Beantworte die Fragen auf dieser [http://www.realmath.de/Neues/Klasse8/hyperbel/hyperbel.html Seite]
−
</div><br>
+
<br>
  
−
Der Funktionsterm von [[bild:f24-x.jpg|center]] ist ein Bruch. Nun kann im Zähler und Nenner eines Bruches auch die Variable x vorkommen. Deshalb definiert man allgemein:
+
Der Funktionsterm von http://wikis.zum.de/rsg/images/0/05/F24-x.jpg ist ein Bruch, in dessen Nenner die Variable <math>x</math> vorkommt.
  
 +
----
  
−
<div style="margin:0;  border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1E1FF; align:left;">
+
Mehr über indirekte Proportionalität findest du in [http://rfdz.ph-noe.ac.at/fileadmin/Mathematik_Uploads/Medienvielfalt/Medienvielfalt3/lernpfad_direktes_indirektes_verhaeltnis/iv_dv_final/index.htm diesem Lernpfad].
−
  Ist der Funktionsterm der Funktion f ein Bruch und stehen in Nenner und/oder Zähler Terme mit der Variablen x, zum Beispiel [[bild:bspl-rationale-funktion.jpg|center]] oder allgemeiner [[bild:bspl-rationale-funktion2.jpg|center]] so heißt diese Funktion '''rationale Funktion'''.
+
−
</div>
+
−
 
+
−
[[Rationale Funktionen/Einführung/Hefteintrag|Hefteintrag]]
+

Version vom 6. April 2013, 15:06 Uhr

Eine Tafel Schokolade mit 24 Stücken soll auf Kinder verteilt werden. Wie viele Stückchen bekommt jedes Kind?

x bezeichne die Anzahl der Kinder und y die Anzahl der Schokoladenstückchen, die jedes Kind bekommt.

  Aufgabe 1  Stift.gif

a) Vervollständige die Tabelle: http://wikis.zum.de/rsg/images/6/67/Tab-24-x.jpg

b) Zeichne den Graph für dieses Beispiel.



a) http://wikis.zum.de/rsg/images/3/31/Tab-24-x-lsg.jpg

b) http://wikis.zum.de/rsg/images/b/bc/24-x.jpg

Betrachte die Produkte x*y, so stellst du fest, dass x*y= 24 ist.

Nuvola apps kig.png   Merke


Eine Zuordnung zwischen zwei Größen x und y heißt indirekt proportional, wenn das Produkt x*y für alle Paare (x,y) stets konstant ist.


In diesem Beispiel ist x eine natürliche Zahl zwischen 1 und 24.

Man kann die Funktion http://wikis.zum.de/rsg/images/0/05/F24-x.jpg allgemein für alle rationalen Zahlen x, die ungleich Null sind, erklären.
Der Graph dieser Funktion schaut dann so aus:

http://wikis.zum.de/rsg/images/6/64/F24-x-graph.jpg

Der Graph einer indirekten Proportionalität heißt Hyperbel.


Nuvola apps kig.png   Merke

Die Funktion http://wikis.zum.de/rsg/images/a/a6/Fm_x_term.jpg mit einer rationalen Zahl m heißt indirekte Proportionalität oder indirekt proportionale Funktion.

  Aufgabe 2  Stift.gif

Bestimme die Definitionsmenge und die Wertemenge.

Ist der Graph symmetrisch bezüglich des Koordinatensystems?


Da x im Nenner steht, darf x nicht 0 sein, also ist die Definitionsmenge 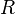R\{0}.

Eine solche Stelle, an der der Funktionsterm nicht definiert ist und in deren Nähe die Funktionswerte nach + Unendlich oder - Unendlich gehen, heißt Polstelle.

http://wikis.zum.de/rsg/images/6/64/F24-x-graph.jpg

Aus dem Graph sieht man, dass 0 als Funktionswert nicht angenommen wird, ansonsten kommen alle reelle Zahlen als y-Werte vor, also ist die Wertemenge auch 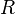R\{0}.

Desweiteren sieht man, dass der Graph punktsymmetrisch zum Ursprung ist.

{{Arbeiten|NUMMER = 3| ARBEIT= a) Stelle in diesem Applet

den Schieberegler für m so ein, dass es den Graphen von http://wikis.zum.de/rsg/images/6/64/F24-x-graph.jpg zeigt.
2. Beantworte die Fragen auf dieser Seite

Der Funktionsterm von http://wikis.zum.de/rsg/images/0/05/F24-x.jpg ist ein Bruch, in dessen Nenner die Variable x vorkommt.

Mehr über indirekte Proportionalität findest du in diesem Lernpfad.

Von „http://medienvielfalt.zum.de/index.php?title=Rationale_Funktionen_Indirekte_Proportionalitaet&oldid=7191“