Rationale Funktionen Indirekte Proportionalitaet: Unterschied zwischen den Versionen
| Zeile 38: | Zeile 38: | ||
{{Merke| | {{Merke| | ||
| − | Die Funktion | + | Die Funktion <math>f:x \rightarrow \frac{m}{x}</math> mit einer reellen Zahl <math>m \not = 0</math> heißt '''indirekte Proportionalität''' oder '''indirekt proportionale Funktion'''. |
}} | }} | ||
| + | |||
{{Arbeiten|NUMMER =2| | {{Arbeiten|NUMMER =2| | ||
ARBEIT= | ARBEIT= | ||
| − | Bestimme die Definitionsmenge und die Wertemenge. | + | Bestimme die Definitionsmenge und die Wertemenge der Funktion <math>f:x \rightarrow \frac{24}{x}</math>. |
Ist der Graph symmetrisch bezüglich des Koordinatensystems? | Ist der Graph symmetrisch bezüglich des Koordinatensystems? | ||
| Zeile 59: | Zeile 60: | ||
Desweiteren sieht man, dass der Graph punktsymmetrisch zum Ursprung ist. | Desweiteren sieht man, dass der Graph punktsymmetrisch zum Ursprung ist. | ||
}} | }} | ||
| + | |||
{{Arbeiten|NUMMER = 3| | {{Arbeiten|NUMMER = 3| | ||
| Zeile 66: | Zeile 68: | ||
den Schieberegler für m so ein, dass es den Graphen von http://wikis.zum.de/rsg/images/0/05/F24-x.jpg zeigt. | den Schieberegler für m so ein, dass es den Graphen von http://wikis.zum.de/rsg/images/0/05/F24-x.jpg zeigt. | ||
| − | b) Beschreibe wie du den Graphen | + | b) Beschreibe wie du den Graphen der Funktion <math>f:x \rightarrow \frac{24}{x}</math> aus dem Graphen der Funktion <math>f:x \rightarrow \frac{1}{x}</math> erhältst? |
c) Beantworte die Fragen auf dieser [http://www.realmath.de/Neues/Klasse8/hyperbel/hyperbel.html Seite] (wird im Mozilla Firefox nicht alles angezeigt, also mit Internet Explorer öffnen!). | c) Beantworte die Fragen auf dieser [http://www.realmath.de/Neues/Klasse8/hyperbel/hyperbel.html Seite] (wird im Mozilla Firefox nicht alles angezeigt, also mit Internet Explorer öffnen!). | ||
<br> | <br> | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | a) m = 24 | ||
| + | |||
| + | b) Jeder y-Wert der Funktion <math>f:x \rightarrow \frac{1}{x}</math> wird mit 24 multiplilziert. Der Graph von <math>f:x \rightarrow \frac{1}{x}</math> wird in y-Richtung um den Faktor 24 gestreckt. | ||
}} | }} | ||
Version vom 7. April 2013, 06:38 Uhr
Eine Tafel Schokolade mit 24 Stücken soll auf Kinder verteilt werden. Wie viele Stückchen bekommt jedes Kind?
x bezeichne die Anzahl der Kinder und y die Anzahl der Schokoladenstückchen, die jedes Kind bekommt.
|
a) Vervollständige die Tabelle: http://wikis.zum.de/rsg/images/6/67/Tab-24-x.jpg b) Zeichne den Graph für dieses Beispiel. c) Betrachte die Produkte |
a) http://wikis.zum.de/rsg/images/3/31/Tab-24-x-lsg.jpg
b)
http://wikis.zum.de/rsg/images/b/bc/24-x.jpg
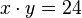 .
.|
|
In diesem Beispiel ist x eine natürliche Zahl zwischen 1 und 24.
Man kann die Funktion 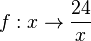 allgemein für alle reellen Zahlen
allgemein für alle reellen Zahlen 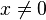 erklären.
erklären.
Der Graph dieser Funktion schaut dann so aus:
|
Die Funktion |
|
Bestimme die Definitionsmenge und die Wertemenge der Funktion Ist der Graph symmetrisch bezüglich des Koordinatensystems? |
Da x im Nenner steht, darf x nicht 0 sein, also ist die Definitionsmenge 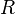 \{
\{ }.
}.
Eine solche Stelle, an der der Funktionsterm nicht definiert ist und in deren Nähe die Funktionswerte nach + Unendlich oder - Unendlich gehen, heißt Polstelle.
Aus dem Graph sieht man, dass 0 als Funktionswert nicht angenommen wird, ansonsten kommen alle reelle Zahlen als y-Werte vor, also ist die Wertemenge auch 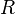 \{
\{ }.
}.
|
a) Stelle in diesem Applet den Schieberegler für m so ein, dass es den Graphen von http://wikis.zum.de/rsg/images/0/05/F24-x.jpg zeigt. b) Beschreibe wie du den Graphen der Funktion c) Beantworte die Fragen auf dieser Seite (wird im Mozilla Firefox nicht alles angezeigt, also mit Internet Explorer öffnen!).
|
Der Funktionsterm von http://wikis.zum.de/rsg/images/0/05/F24-x.jpg ist ein Bruch, in dessen Nenner die Variable  vorkommt. Kommen im Nenner der Funktion
vorkommt. Kommen im Nenner der Funktion  auch andere Terme mit
auch andere Terme mit  vor, z.B.
http://wikis.zum.de/rsg/images/e/eb/Bspl-rationale-funktion.jpg oder http://wikis.zum.de/rsg/images/d/dd/Bspl-rationale-funktion2.jpg
vor, z.B.
http://wikis.zum.de/rsg/images/e/eb/Bspl-rationale-funktion.jpg oder http://wikis.zum.de/rsg/images/d/dd/Bspl-rationale-funktion2.jpg
dann spricht man von rationalen Funktionen.
Internetlinks:
Mehr über indirekte Proportionalität wiederholst du in diesem Lernpfad.
Alles über Hyperbeln
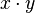 . Was stellst du fest?
. Was stellst du fest?
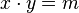 .
.
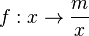 mit einer reellen Zahl
mit einer reellen Zahl 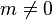 heißt indirekte Proportionalität oder indirekt proportionale Funktion.
heißt indirekte Proportionalität oder indirekt proportionale Funktion.
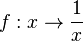 erhältst?
erhältst?

