Trigonometrische Funktionen: Unterschied zwischen den Versionen
| Zeile 59: | Zeile 59: | ||
[[Bild:sin_b.jpg|center]] | [[Bild:sin_b.jpg|center]] | ||
Man erhält den Graph der Funktion f: x---> sin(bx) aus dem Graph der Sinusfunktion sin durch | Man erhält den Graph der Funktion f: x---> sin(bx) aus dem Graph der Sinusfunktion sin durch | ||
| − | b > 1: Stauchung in x-Richtung | + | b > 1: Stauchung in x-Richtung |
| − | 0 < b < 1: Streckung in x-Richtung. | + | |
| + | 0 < b < 1: Streckung in x-Richtung. | ||
| + | |||
Bei negativem b ist wegen sin(-x) = - sin(x) der Graph noch an der x-Achse zu spiegeln. | Bei negativem b ist wegen sin(-x) = - sin(x) der Graph noch an der x-Achse zu spiegeln. | ||
}} | }} | ||
| Zeile 80: | Zeile 82: | ||
a > 0: Multiplikation aller Werte mit dem Faktor a, also für <br> | a > 0: Multiplikation aller Werte mit dem Faktor a, also für <br> | ||
0 < a < 1: Stauchung um den Faktor a | 0 < a < 1: Stauchung um den Faktor a | ||
| + | |||
1 < a: Streckung um den Faktor a | 1 < a: Streckung um den Faktor a | ||
Version vom 8. Juni 2008, 06:31 Uhr
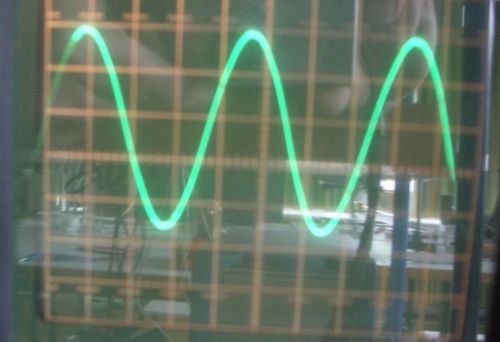
Oftmals sieht man auf einem Oszilloskop ein solches Bild:
Was kann man dort ablesen? Wie erhält man aus dem Bild die nötigen Informationen?
Man muss Nullstellen, maximale Amplitude, Abstände ... aus der angezeigten Kurve erkennen und ablesen.
Um ein solches Bild am Oszilloskop richtig zu interpretieren muss man verschiedene Sinusfunktionen f: x ---> a sin(b*x+c)+d betrachten. Welche Bedeutung haben dort die Parameter a, b, c, d?
In diesem Bild.jpg)
Du kennst die Nullstellen der Sinusfunktion. Wo sind sie?
Stelle in der Zeichnung fest an welchen Stellen der Graph der schwarzen Funktion Nullstellen hat und notiere sie.
In der Funktion f: x---> a sin(bx - c) + d sind a, b, c, d Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen.
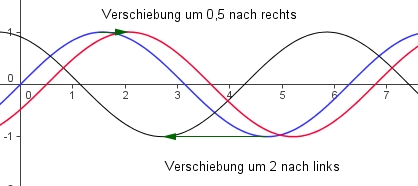
Einfluss von d: f: x---> sin(x)+d
Bearbeite dieses Arbeitsblatt und beantworte die dort gestellten Fragen.
Hier kannst du dein Wissen überprüfen.
Formuliere dein Ergebnis über den Einfluss von d in f: x---> sin(x)+d
Hefteintrag
Man erhält den Graph der Funktion f: x---> sin(x)+d aus dem Graph der Sinusfunktion sin durch Verschiebung um d in Richtung der y-Achse.
Übertrage deine Ergebnisse auf cos(x)+d
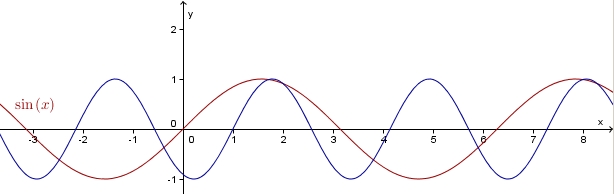
Einfluss von c: f: x---> sin(x-c)
Bearbeite wie eben dieses Arbeitsblatt, beantworte die Fragen und überprüfe hier.
Formuliere dein Ergebnis über den Einfluss von d in f: x---> sin(x-c)
Hefteintrag
Man erhält den Graph der Funktion f: x---> sin(x-c) aus dem Graph der Sinusfunktion sin durch Verschiebung um c in Richtung der x-Achse.
Übertrage deine Ergebnisse auf cos(x-c)
Hier kannst beide Parameter c und d durch Verschieben des Graphen ändern und die Auswirkung auf den Funktionsterm betrachten.
Übertrage deine Ergebnisse auf cos(x-c)+d
Einfluss von b: f: x---> sin(bx)
Bearbeite wie eben dieses Arbeitsblatt, beantworte die Fragen und überprüfe hier.
Formuliere dein Ergebnis über den Einfluss von d in f: x---> sin(bx)
Hefteintrag
Übertrage deine Ergebnisse auf cos(bx)
Man erhält den Graph der Funktion f: x---> sin(bx) aus dem Graph der Sinusfunktion sin durch
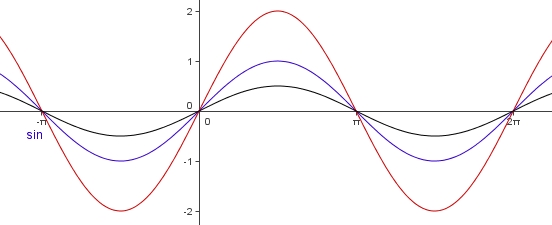
Einfluss von a: f: x---> a sin(x)
Auf diesem Arbeitsblatt variierst du mit dem Schieberegler den Parameter a und beobachtest die Auswirkung auf den Graphen. Beantworte die dort gestellten Aufgaben.
Formuliere dein Ergebnis über den Einfluss von d in f: x---> a sin(x)
Hefteintrag
Man erhält den Graph der Funktion f: x---> a sin(x) aus dem Graph der Sinusfunktion sin durch
a > 0: Multiplikation aller Werte mit dem Faktor a, also für
0 < a < 1: Stauchung um den Faktor a
1 < a: Streckung um den Faktor a
Für negative a (a < 0) muss man den Graph noch an der x-Achse spiegeln.
Übertrage deine Ergebnisse auf a cos(x)
Zusammenfassung:
In diesem Arbeitsblatt variierst du durch Schieberegler die verschiedenen Parameter. Beobachte die Auswirkung auf den Graphen.
Bearbeite die Aufgaben dieses Arbeitsblattes.
Finde zu den Graphen auf diesem Arbeitsblatt die zugehörigen Funktionsterme.
Was fällt auf, wenn du hier für b > 1 den Parameter c änderst?
In dem Applet auf dieser Seite werden die Parameter b und c anders verwendet. Finde den Unterschied zu den bisherigen Betrachtungen heraus.
Übertrage deine Ergebnisse auf a cos(bx-c)+d beziehungsweise a cos[b(x-c)]+d
Anwendungen:
- In dem Applet auf dieser Seite ist die Entstehung einer Schwingung dargestellt. Mit dem Schieberegler für t kannst du die Schwingung darstellen. Überlege dir die gestellten Aufgaben und finde dann mit den angegebenen Größen y_max und T einen Funktionsterm für die zugehörige Sinusschwingung.
- In dem Applet auf diesem Arbeitsblatt werden die Parameter einer Sinusschwingung aus der Physik behandelt. Welche Parameter a,b,c,d entsprechen welchen physikalischen Größen a, f, phi_0?
- Finde zu den Parametern a, b, c, d aus diesem Arbeitsblatt zur harmonischen Schwingung deren entsprechende Größen.
