Quadratische Funktionen 2 Einfluss von b: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 64: | Zeile 64: | ||
---- | ---- | ||
'''Aufgabe B1:''' {{Lösung versteckt| | '''Aufgabe B1:''' {{Lösung versteckt| | ||
| − | :Man erhält den Graph der Funktion | + | :Man erhält den Graph der Funktion <math> f: x \rightarrow x^2 + bx</math> |
:aus dem Graph der Quadratfunktion <math>q: x \rightarrow x^2 </math> durch Verschiebung sowohl in x- wie auch in y-Richtung | :aus dem Graph der Quadratfunktion <math>q: x \rightarrow x^2 </math> durch Verschiebung sowohl in x- wie auch in y-Richtung | ||
| Zeile 72: | Zeile 72: | ||
:* Ist b > 0, so wird die Normalparabel schräg nach links unten verschoben. | :* Ist b > 0, so wird die Normalparabel schräg nach links unten verschoben. | ||
:* Ist b < 0, so wird die Normalparabel schräg nach recht unten verschoben. | :* Ist b < 0, so wird die Normalparabel schräg nach recht unten verschoben. | ||
| − | :* Je größer der Betrag von | + | :* Je größer der Betrag von b ist, desto mehr wird in y-Richtung verschoben |
:* Der Graph zu -b ist spiegelsymmetrisch bezüglich der y-Achse zum Graph von b. | :* Der Graph zu -b ist spiegelsymmetrisch bezüglich der y-Achse zum Graph von b. | ||
| − | :* Die Scheitel aller Graphen zu <math>f: x \rightarrow x^2 + bx</math> liegen auf der dem Graphen der Funktion <math>-q: x \rightarrow -x^2</math> }} | + | :* Die Scheitel aller Graphen zu <math> f: x \rightarrow x^2 + bx</math> liegen auf der dem Graphen der Funktion <math>-q: x \rightarrow -x^2</math> }} |
'''Aufgabe B2:''' {{Lösung versteckt|1= | '''Aufgabe B2:''' {{Lösung versteckt|1= | ||
Version vom 27. August 2011, 10:36 Uhr
Zurück zu 6. Allgemeine quadratische Funktion
|
Wir betrachten nun den Einfluss von
Aufgabe B1:
Aufgabe B2:
Aufgabe B3:
Aufgabe B4:
Hefteintrag: Beachte, dass in der Lösung zur Aufgabe B1 ein Hefteintrag "versteckt" ist! Zurück zu 6. Allgemeine quadratische Funktion |
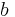 in
in 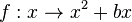 .
.
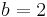 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 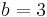 und
und 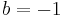 sowie
sowie 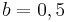 auf den Graphen auswirken und überprüfe deine Vermutung.
auf den Graphen auswirken und überprüfe deine Vermutung. 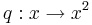 durch Verschiebung sowohl in x- wie auch in y-Richtung
durch Verschiebung sowohl in x- wie auch in y-Richtung