Eigenschaften von Funktionen: Unterschied zwischen den Versionen
(→Monotonie) |
|||
| Zeile 58: | Zeile 58: | ||
{{Merke| | {{Merke| | ||
Eine Funktionsgraph <math> G_f</math> heißt '''streng monoton steigend''' im Intervall [a;b], wenn die Funktion <math>f</math> dort streng monoton zunehmend ist, <br> | Eine Funktionsgraph <math> G_f</math> heißt '''streng monoton steigend''' im Intervall [a;b], wenn die Funktion <math>f</math> dort streng monoton zunehmend ist, <br> | ||
| − | d.h.für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) | + | d.h.für alle <math> x_1,x_2 \in [a;b]</math> gilt: <math>x_1 < x_2 \Rightarrow f(x_1) < f(x_2)</math> |
Eine Funktionsgraph <math> G_f</math> heißt '''streng monoton fallend''' im Intervall [a;b], wenn die Funktion <math>f</math> dort streng monoton abnehmend ist, <br> | Eine Funktionsgraph <math> G_f</math> heißt '''streng monoton fallend''' im Intervall [a;b], wenn die Funktion <math>f</math> dort streng monoton abnehmend ist, <br> | ||
Version vom 2. Januar 2012, 08:25 Uhr
Monotonie
Dieser Begriff des Ansteigens eines Funktionsgraphen fassen wir genauer und benennen ihn.
|
Eine Funktion |
Auch diesen Begriff des Fallens eines Funktionsgraphen fassen wir - analog zu oben - genauer und benennen ihn.
|
Eine Funktion |
Man könnte diese Begriffe monoton zunehmend und monoton abnehmend auch für die Funktionsgraphen übernehmen, hier verwendet man allerdings monoton steigend und monoton fallend.
|
Eine Funktionsgraph Eine Funktionsgraph |
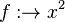 in
in 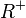
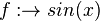 in [0;1]
in [0;1] 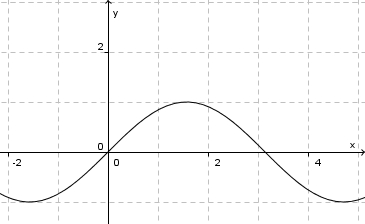
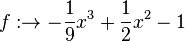 in [0;3]
in [0;3] 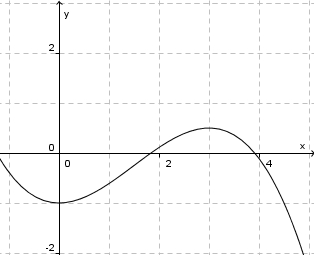
 heißt streng monoton zunehmend im Intervall [a;b], wenn für alle
heißt streng monoton zunehmend im Intervall [a;b], wenn für alle ![x_1,x_2 \in [a;b]](/images/math/4/8/9/489a4ad3c2410297428c10a130e7cc95.png) gilt:
gilt: 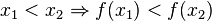
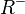
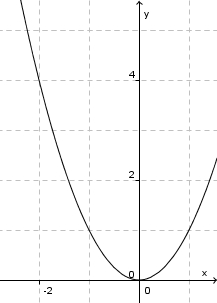
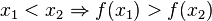
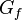 heißt streng monoton steigend im Intervall [a;b], wenn die Funktion
heißt streng monoton steigend im Intervall [a;b], wenn die Funktion 
