Eigenschaften von Funktionen: Unterschied zwischen den Versionen
(→Grenzwert) |
|||
| Zeile 126: | Zeile 126: | ||
=Grenzwert= | =Grenzwert= | ||
| − | {{ | + | {{Merke| |
| − | + | Zuerst vereinbaren wir: | |
| − | + | ||
| − | + | sehr große positve Zahlen sind solche positive Zahlen mit großem Betrag (z.B. 1000000)<br> | |
| + | sehr großen negative Zahlen sind solche negative Zahlen mit großem Betrag (z.B. –1000000) | ||
| + | |||
| + | sehr kleine positive Zahlen sind solche positive Zahlen mit kleinem Betrag (z.B. 0,0000001)<br> | ||
| + | sehr kleinen negative Zahlen solche negative Zahlen mit kleinem Betrag (z.B. –0,0000001 ) | ||
| + | |||
| + | Grenzwerte von Funktionen spiegeln das Verhalten im Unendlichen wieder oder, falls wir x gegen einen anderen Wert als unendlich laufen lassen, das entsprechende Verhalten. | ||
| + | |||
| + | '''Beispiel:''' Wir betrachten die Funktion <math> f: x \rightarrow x^2</math> | ||
| + | |||
| + | Wir wollen x gegen unendlich und gegen minus unendlich laufen lassen. | ||
| + | |||
| + | Wir schreiben für x gegen unendlich: <math>\lim_{n \to \infty}x^2</math> | ||
| + | |||
| + | und für x gegen minus unendlich: <math>\lim_{n \to -\infty}x^2</math> | ||
| + | |||
| + | Es ist dann <math>\lim_{n \to \infty}x^2 = \infty</math> und <math>\lim_{n \to -\infty}x^2 =\infty</math> | ||
| + | |||
| + | Ein Plus-oder Minuszeichen rechts hochgestellt an einer Zahl bei Grenzwerten bedeutet Annäherung von rechts – bzw. von links her an die Zahl | ||
| + | |||
| + | <math>\lim_{n \to 3^+}x^2</math> heißt: x ist bei der Annäherung größer als 3, also z.B. 3,1 ; 3,01 ; 3,001 usw. | ||
| + | |||
| + | <math>\lim_{n \to 3^-}x^2</math> heißt: x ist bei der Annäherung kleiner als 3, also z.B. 2,9 ; 2,99 ; 2,999 usw. | ||
}} | }} | ||
=Symmetrie zum Koordinatensystem= | =Symmetrie zum Koordinatensystem= | ||
Version vom 2. Januar 2012, 15:46 Uhr
Du hast nun Funktionen als Objekte in der Mathematik kennengelernt. Wir wollen als Nächstes untersuchen, welche Eigenschaften Funktionen haben.
Monotonie
Dieser Begriff des Ansteigens eines Funktionsgraphen fassen wir genauer und benennen ihn.
|
Eine Funktion |
Auch diesen Begriff des Fallens eines Funktionsgraphen fassen wir - analog zu oben - genauer und benennen ihn.
|
Eine Funktion |
Man könnte diese Begriffe monoton zunehmend und monoton abnehmend auch für die Funktionsgraphen übernehmen, hier verwendet man allerdings monoton steigend und monoton fallend.
|
Eine Funktionsgraph Eine Funktionsgraph |
|
Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen! |
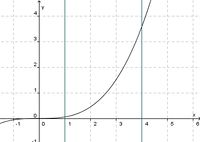 (streng monoton steigend) (!streng monoton fallend) (!weder noch)
(streng monoton steigend) (!streng monoton fallend) (!weder noch)
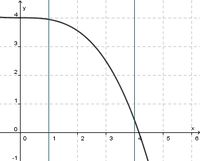 (!streng monoton steigend) (streng monoton fallend) (!weder noch)
(!streng monoton steigend) (streng monoton fallend) (!weder noch)
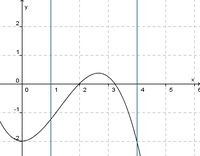 (!streng monoton steigend) (!streng monoton fallend) (weder noch)
(!streng monoton steigend) (!streng monoton fallend) (weder noch)
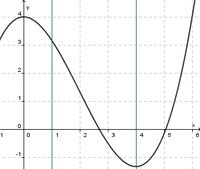 (!streng monoton steigend) (streng monoton fallend) (!weder noch)
(!streng monoton steigend) (streng monoton fallend) (!weder noch)
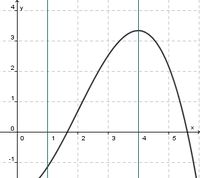 (streng monoton steigend) (!streng monoton fallend) (!weder noch)
(streng monoton steigend) (!streng monoton fallend) (!weder noch)
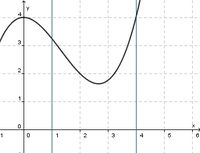 (!streng monoton steigend) (!streng monoton fallend) (weder noch)
(!streng monoton steigend) (!streng monoton fallend) (weder noch)
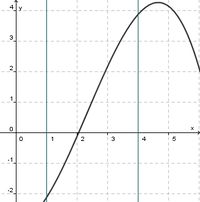 (streng monoton steigend) (!streng monoton fallend) (!weder noch)
(streng monoton steigend) (!streng monoton fallend) (!weder noch)
Für die folgende Multiple-Choice-Aufgabe kannst du als Hilfe GeoGebra öffnen, dir die Graphen der Funktionen zeichnen lassen und dann die Fragen beantworten.
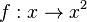 im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
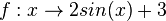 im Intervall [
im Intervall [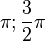 ]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
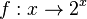 im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
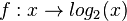 im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
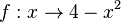 im Intervall [-1;4]
(!streng monoton zunehmend) (!streng monoton abnehmend) (weder noch)
im Intervall [-1;4]
(!streng monoton zunehmend) (!streng monoton abnehmend) (weder noch)
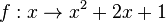 im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
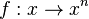 mit
mit 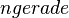 im Intervall [-4;-1]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
im Intervall [-4;-1]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
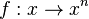 mit
mit 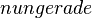 im Intervall [-3;9]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [-3;9]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
Grenzwert
|
Zuerst vereinbaren wir: sehr große positve Zahlen sind solche positive Zahlen mit großem Betrag (z.B. 1000000) sehr kleine positive Zahlen sind solche positive Zahlen mit kleinem Betrag (z.B. 0,0000001) Grenzwerte von Funktionen spiegeln das Verhalten im Unendlichen wieder oder, falls wir x gegen einen anderen Wert als unendlich laufen lassen, das entsprechende Verhalten. Beispiel: Wir betrachten die Funktion Wir wollen x gegen unendlich und gegen minus unendlich laufen lassen. Wir schreiben für x gegen unendlich: und für x gegen minus unendlich: Es ist dann Ein Plus-oder Minuszeichen rechts hochgestellt an einer Zahl bei Grenzwerten bedeutet Annäherung von rechts – bzw. von links her an die Zahl
|
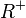
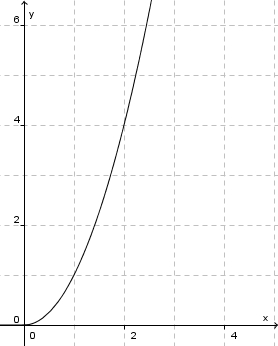
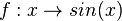 in [0;1]
in [0;1] 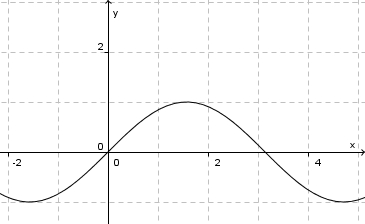
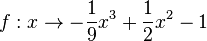 in [0;3]
in [0;3] 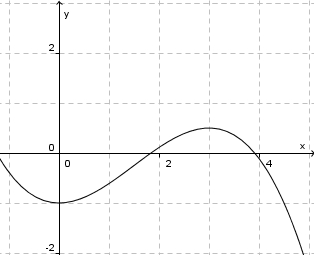
 heißt streng monoton zunehmend im Intervall [a;b], wenn für alle
heißt streng monoton zunehmend im Intervall [a;b], wenn für alle ![x_1,x_2 \in [a;b]](/images/math/4/8/9/489a4ad3c2410297428c10a130e7cc95.png) gilt:
gilt: 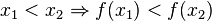
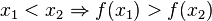
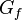 heißt streng monoton steigend im Intervall [a;b], wenn die Funktion
heißt streng monoton steigend im Intervall [a;b], wenn die Funktion 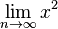
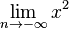
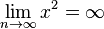 und
und 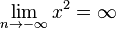
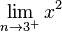 heißt: x ist bei der Annäherung größer als 3, also z.B. 3,1 ; 3,01 ; 3,001 usw.
heißt: x ist bei der Annäherung größer als 3, also z.B. 3,1 ; 3,01 ; 3,001 usw.
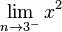 heißt: x ist bei der Annäherung kleiner als 3, also z.B. 2,9 ; 2,99 ; 2,999 usw.
heißt: x ist bei der Annäherung kleiner als 3, also z.B. 2,9 ; 2,99 ; 2,999 usw.

