Symmetrie: Unterschied zwischen den Versionen
| Zeile 16: | Zeile 16: | ||
Im folgenden Applet ist ein Punkt A auf der Normalparabel an der y-Achse gespiegelt. Der Spiegelpunkt ist A'. | Im folgenden Applet ist ein Punkt A auf der Normalparabel an der y-Achse gespiegelt. Der Spiegelpunkt ist A'. | ||
| − | 2. Überprüfe indem du den Punkt A bewegst, ob der Funktionsgraph der Quadratfunktion achsensymmetrisch zur y-Achse ist. | + | 2. Überprüfe indem du den Punkt A bewegst, ob der Funktionsgraph der Quadratfunktion <math>f:x \rightarrow x^2</math> achsensymmetrisch zur y-Achse ist. |
<center> | <center> | ||
| Zeile 24: | Zeile 24: | ||
Im folgenden Applet ist ein Punkt A auf der Kubikparabel am Usprung gespiegelt. Der Spiegelpunkt ist A'. | Im folgenden Applet ist ein Punkt A auf der Kubikparabel am Usprung gespiegelt. Der Spiegelpunkt ist A'. | ||
| − | 3. Überprüfe indem du den Punkt A bewegst, ob der Funktionsgraph der Kubikfunktion punktsymmetrisch zum Ursprung ist. | + | 3. Überprüfe indem du den Punkt A bewegst, ob der Funktionsgraph der Kubikfunktion <math>f:x \rightarrow x^3</math> punktsymmetrisch zum Ursprung ist. |
<center> | <center> | ||
Version vom 3. Januar 2012, 18:00 Uhr
zurück zu Eigenschaften von Funktionen
|
Schau dir diesen Video an:
Im folgenden Applet ist ein Punkt A auf der Normalparabel an der y-Achse gespiegelt. Der Spiegelpunkt ist A'. 2. Überprüfe indem du den Punkt A bewegst, ob der Funktionsgraph der Quadratfunktion
Im folgenden Applet ist ein Punkt A auf der Kubikparabel am Usprung gespiegelt. Der Spiegelpunkt ist A'. 3. Überprüfe indem du den Punkt A bewegst, ob der Funktionsgraph der Kubikfunktion
|
|
Merke:
|
Im folgenden Video siehst du weitere Beispiele zur Symmetrie:
zurück zu Eigenschaften von Funktionen
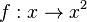 achsensymmetrisch zur y-Achse ist.
achsensymmetrisch zur y-Achse ist.
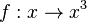 punktsymmetrisch zum Ursprung ist.
punktsymmetrisch zum Ursprung ist.

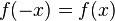 ist. Die Funktion
ist. Die Funktion  heißt gerade.
heißt gerade.
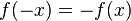 ist. Die Funktion
ist. Die Funktion 
