Symmetrie: Unterschied zwischen den Versionen
| Zeile 40: | Zeile 40: | ||
<center>>{{#ev:youtube |gL3ea3Nbz_Y|350}}</center> | <center>>{{#ev:youtube |gL3ea3Nbz_Y|350}}</center> | ||
| + | {{Arbeiten| | ||
| + | NUMMER=2| | ||
| + | ARBEIT= Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen! | ||
| + | }} | ||
| + | <div class="multiplechoice-quiz"> | ||
| + | [[Bild:Symmetrie_f1.jpg|200px]] | ||
| + | (achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (!weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f3.jpg|200px]] | ||
| + | (achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (!weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f5.jpg|200px]] | ||
| + | (!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f7.jpg|200px]] | ||
| + | (!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f9.jpg|200px]] | ||
| + | (!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f2.jpg|200px]] | ||
| + | (achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (!weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f4.jpg|200px]] | ||
| + | (!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f6.jpg|200px]] | ||
| + | (!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f9a.jpg|200px]] | ||
| + | (!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f8.jpg|200px]] | ||
| + | (!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch) | ||
| + | |||
| + | [[Bild:Symmetrie_f9b.jpg|200px]] | ||
| + | (!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | Für die folgende Multiple-Choice-Aufgabe kannst du als Hilfe GeoGebra öffnen, dir die Graphen der Funktionen zeichnen lassen und dann die Fragen beantworten. | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | <math>f:x \rightarrow x^2</math> im Intervall [2;8] | ||
| + | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch) | ||
| + | |||
| + | <math>f:x \rightarrow 2sin(x) + 3 </math> im Intervall [<math>\pi;\frac{3}{2}\pi</math>] | ||
| + | (!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch) | ||
| + | |||
| + | <math>f:x \rightarrow 2^x </math> im Intervall [-1;4] | ||
| + | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch) | ||
| + | |||
| + | <math>f:x \rightarrow log_2(x) </math> im Intervall [-1;4] | ||
| + | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch) | ||
| + | |||
| + | <math>f:x \rightarrow 4-x^2 </math> im Intervall [-1;4] | ||
| + | (!streng monoton zunehmend) (!streng monoton abnehmend) (weder noch) | ||
| + | |||
| + | <math>f:x \rightarrow x^2+2x+1</math> im Intervall [2;8] | ||
| + | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch) | ||
| + | |||
| + | <math>f:x \rightarrow x^n</math> mit <math> n gerade</math> im Intervall [-4;-1] | ||
| + | (!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch) | ||
| + | |||
| + | <math>f:x \rightarrow x^n</math> mit <math> n ungerade</math> im Intervall [-3;9] | ||
| + | (streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch) | ||
| + | |||
| + | </div> | ||
---- | ---- | ||
zurück zu [[Funktionen_Einstieg/Eigenschaften von Funktionen|Eigenschaften von Funktionen]] | zurück zu [[Funktionen_Einstieg/Eigenschaften von Funktionen|Eigenschaften von Funktionen]] | ||
Version vom 4. Januar 2012, 09:51 Uhr
zurück zu Eigenschaften von Funktionen
|
Schau dir diesen Video an:
Im folgenden Applet ist ein Punkt A auf der Normalparabel an der y-Achse gespiegelt. Der Spiegelpunkt ist A'. 2. Überprüfe indem du den Punkt A bewegst, ob der Funktionsgraph der Quadratfunktion
Im folgenden Applet ist ein Punkt A auf der Kubikparabel am Usprung gespiegelt. Der Spiegelpunkt ist A'. 3. Überprüfe indem du den Punkt A bewegst, ob der Funktionsgraph der Kubikfunktion
|
|
Merke:
|
Im folgenden Video siehst du je ein Beispiel einer Polynomfunktion zur Achsensymmetrie und zur Punktsymmetrie und es wird ausführlich erklärt, wie du dies durch Rechnung überprüfen kannst.
|
Teste dich! Klicke im folgenden Quiz auf die richtigen Zuordnungen! |
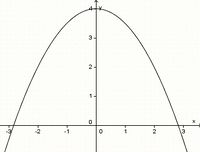 (achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (!weder noch)
(achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (!weder noch)
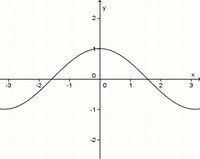 (achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (!weder noch)
(achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (!weder noch)
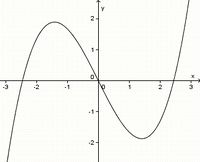 (!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch)
(!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch)
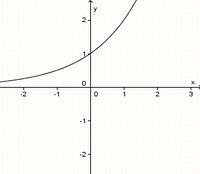 (!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch)
(!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch)
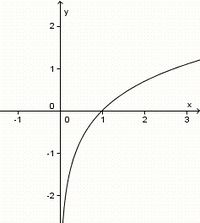 (!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch)
(!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch)
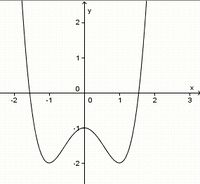 (achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (!weder noch)
(achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (!weder noch)
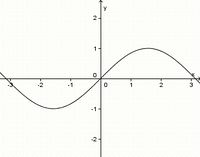 (!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch)
(!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch)
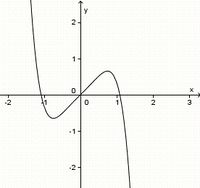 (!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch)
(!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch)
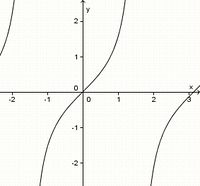 (!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch)
(!achsensymmetrisch zur y-Achse) (punktsymmetrisch zum Ursprung) (!weder noch)
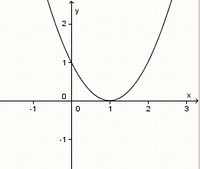 (!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch)
(!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch)
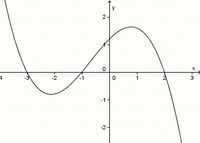 (!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch)
(!achsensymmetrisch zur y-Achse) (!punktsymmetrisch zum Ursprung) (weder noch)
Für die folgende Multiple-Choice-Aufgabe kannst du als Hilfe GeoGebra öffnen, dir die Graphen der Funktionen zeichnen lassen und dann die Fragen beantworten.
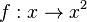 im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
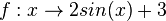 im Intervall [
im Intervall [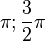 ]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
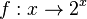 im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
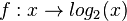 im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [-1;4]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
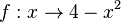 im Intervall [-1;4]
(!streng monoton zunehmend) (!streng monoton abnehmend) (weder noch)
im Intervall [-1;4]
(!streng monoton zunehmend) (!streng monoton abnehmend) (weder noch)
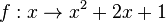 im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [2;8]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
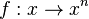 mit
mit 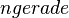 im Intervall [-4;-1]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
im Intervall [-4;-1]
(!streng monoton zunehmend) (streng monoton abnehmend) (!weder noch)
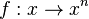 mit
mit 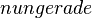 im Intervall [-3;9]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
im Intervall [-3;9]
(streng monoton zunehmend) (!streng monoton abnehmend) (!weder noch)
zurück zu Eigenschaften von Funktionen
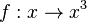 punktsymmetrisch zum Ursprung ist.
punktsymmetrisch zum Ursprung ist.

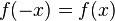 ist. Die Funktion
ist. Die Funktion  heißt gerade.
heißt gerade.
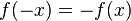 ist. Die Funktion
ist. Die Funktion 
