Wurzelfunktion Anwendungen: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher wird | + | Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher wird zuerst die Funktion <math> f: x \rightarrow a \sqrt x </math> betrachtet. |
{{Arbeiten| | {{Arbeiten| | ||
Version vom 28. Januar 2012, 10:58 Uhr
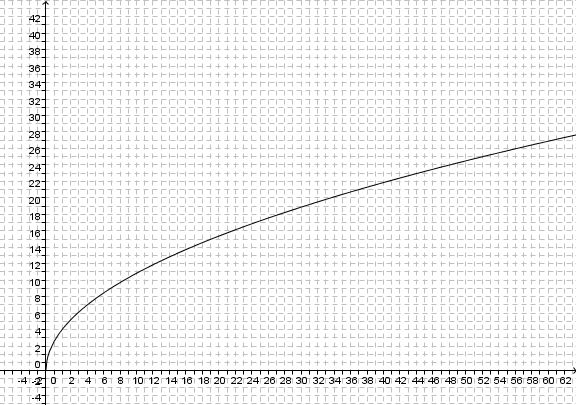
Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher wird zuerst die Funktion 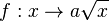 betrachtet.
betrachtet.
|
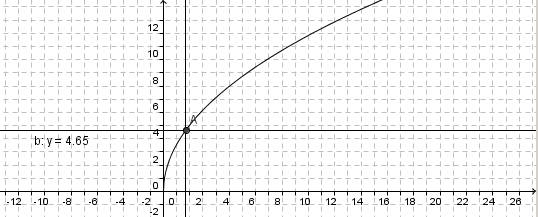
Im Applet ist der Graph der Wurzelfunktion Wie ändert sich der Graph der Wurzelfunktion
|
- Für a = -1 wird der Graph der Wurzelfunktion
 an der x-Achse gespiegelt.
an der x-Achse gespiegelt.
- Für 0 < a < 1 wird der Graph der Wurzelfunktion
 in y-Richtung gestaucht.
in y-Richtung gestaucht.
- Für 1 < a wir der Graph der Wurzelfunktion
 in y-Richtung gestreckt.
in y-Richtung gestreckt.
- Für negative a wird der Graph von 2. oder 3. an der y-Achse gespiegelt.
|
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
|
|
Schau dir diesen Video an. Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann man bei guten Bedingungen durch die Formel
|
Zurück zu Wurzelfunktion oder weiter mit Übungen.
 dargestellt.
dargestellt.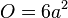
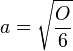
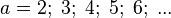
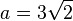
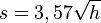 (vgl.
(vgl. 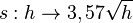 .
.