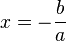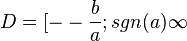Wurzelfunktion Übungen 1: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 18: | Zeile 18: | ||
{{Arbeiten| | {{Arbeiten| | ||
NUMMER=2| ARBEIT= | NUMMER=2| ARBEIT= | ||
| + | Du betrachstest die Funktion <math>f: x \rightarrow \sqrt{ax + b} </math>. Im folgenden Applet kannst du mit den Schiebereglern die Werte für <math>a</math> und <math>b</math> verändern. Anfangs ist <math>a = 1</math> und <math>b = 0</math>. Es ist der Graph der Quadratwurzelfunktion dargestellt. | ||
| + | :1. Was passiert, wenn du den Wert von <math>b</math> änderst? Unterscheide <math> b > 0 </math> und <math> b < 0</math>. | ||
| + | :2. Stelle wieder <math> b = 0</math> ein. Variiere nun <math>a</math>. Was stellst du fest? | ||
| + | <ggb_applet width="792" height="407" version="4.0" ggbBase64="UEsDBBQACAAIALaAPEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIALaAPEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VdZj9s2EH5OfsVAT0kbr0VdtgM5QZMi6AKbpMCmRdE3SqJlZiVRJSlbG+THd0hKsrw5miBtgdZYL6/h3N9wnD7t6woOTCoumq1HLnwPWJOLgjfl1uv0brH2nj65n5ZMlCyTFHZC1lRvvchQ8mLrJVno+8E6WoQJDRZRQPzFZh2wxYblO5IkSbgqEg+gV/xxI17RmqmW5uw637OaXomcait4r3X7eLk8Ho8Xo6gLIctlWWYXvSo8QDUbtfWGyWNkd3bpGFrywPfJ8reXV479gjdK0yZnHhgTOv7k/r30yJtCHOHIC73femsfzdgzXu7RpjiMPVgaohYd0rJc8wNTeHW2tDbruvUsGW3M+T03g2oyx4OCH3jB5NbzLwLkKiRnjR5OySBlOd5PD5wdHSMzszIiD7QQVUYND3j/HgI/8OGRGYgbAhySxB35bs8P3RC4IXJD7Ggidz1ypJGjiRxNFHpw4IpnFdt6O1op9BlvdhLjNa2Vvq2Y1WfYONlLHqFNir9D4tB41DkZ933/kfkm+I3MwfLcSDKTqmX3lUJHkfF69eUig28RGY4ig49ZGcSfsDL5jHOdDl9iJolnMlGU/bPfDySGwVdIdOtvE5hE/4qJ6XJESjqAA9Te0A6R1KxWBi7hBuKNyXoCMUIjWWGSx0A2OKwCQDAAiSGKcUnWkJhxBeEKDyIIYQ2GjoRgsRGv8V+0sswSiJGZ2V0hJIGgoAjiEIiFVAQIJLCwRIgGIVLEMcR4yYgngWERJhAluArXEKGOBpErgoQhXsQ1ig8gJBCay2QFQQKJ4Ucig/RkbVRHlgEkPiTEMERQI6AdmJF+DaGxJhncxZu202cuyutinGrRTrFAaixHpzLnytNZFbyXVjRjFT4M1yaSAAdaGURYQTvRaBiDGLi9UtJ2z3N1zbTGWwre0gO9opr1L5BajbItbS4a9bMU+rmourpRALmo/ElnUZHZPJi0xkU4O4jmB/HsIJnNVx+VK/AEOsVQvpBqJKdFcWkoTqUBPfm6qW6fSUZvWsHPzUiX9o1JWZdXvOC0+RWT1UgxfoHxybHVanxywvVmVETI4vpWYQZD/zuTAmsMic0je+tWoVnNPxhjlVODt9i3dLPV/EOcAHaY4kB7NplYSl7M55fqmaiKyWBr43Pa6k7ajgALoDSa/9CUFbN5YCsqPrf5TSb6a5cAoeP15rbFle/kZ6X1LSD+gxhfxHIYMzdaGqPYROVbGt9S+GNG8WI6J5vAUtgxc6OlwhR1qg2GktFK4o9iuLJVy/fOsGHz2zzeXcP11bjQPL8ZLCWO/lVXZ+yUJYbgR+46DddCnUsh/5yUdHkn19IbJhtWDamN4e5EpxxSZ1lfsJzXuHQHg9uoCekvqJPbLVgp2UBPK9uROafaU3+etR9sW1YvpKgvm8MbzJc7CqTLUctU5ZK3Jishw+fghp0yr+CK4mtSzO8ZLKI3cvNqoEO08RaitNN7IW3ThcUFRwPBitXYcIG2Kdh0NZM8n3xPbfeGSnWD3lPQjONBZG+x6t2Jl11YGjz+RJICrdo9NT3fALqK3jJ55hrL7aUoRsGD2Mo0i1BzfAwXCIqa9ghk5JcpLIga22WMRXNql51mQ0HB1sPgvze9ly0EY0XY8X7mUPQRf4c5Qc+MOYFFY62+wX5UWUTrAbt28hMvCtZM2tIGs8fGAMtV68wFfCmYS/bpaovm26oxi/wQmL8MUXY3RP7/LESb/0KI+laiNMNmcPEOfx72pm140D+ELag/pH5A4Tvo4XvIHro+4jywu66xePVOLP7OKPqfjeLr3U4xbfweWacv1p+N8dd7eu6t5bw82W5g+CX75E9QSwcIqF1m+mMFAABmDwAAUEsBAhQAFAAIAAgAtoA8QNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAC2gDxAqF1m+mMFAABmDwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAPoFAAAAAA==" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br> | ||
| + | :3. Variiere nun a und b gleichzeitig und beachte was passiert. | ||
| + | :4. Wo ist die Nullstelle der Funktion <math>f: x \rightarrow \sqrt{ax + b} </math>? | ||
| + | :5. Gib die Definitionsmenge der Funktion <math>f: x \rightarrow \sqrt{ax + b} </math> an. | ||
}} | }} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| + | 1. Für <math> b > 0 </math> wird der Graph der Wurzelfunktion nach links verschoben. Die Nullstelle tritt bei <math> x = -b</math> auf. Für <math> b < 0</math> wird der Graph der Wurzelfunktion nach rechts verschoben. Die Nullstelle tritt bei <math> x = -b</math> auf. | ||
| + | |||
| + | 2. Für <math> 0 < a < 1</math> wird der Graph der Wurzelfunktion in y-Richtung gestaucht. Für <math> a > 1</math> wird der Graph in y-Richtung gestreckt. Ist <math> a < 0</math> so wird der Graph mit <math>|a|</math> an der y-Achse gespiegelt. | ||
| + | |||
| + | 4. <math>x = -\frac{b}{a}</math> | ||
| + | |||
| + | 5. <math>D = [--\frac{b}{a};sgn(a) \infty </math> | ||
}} | }} | ||
Version vom 28. Januar 2012, 17:23 Uhr
Bei den Übungen zur Wurzelfunktion ...
|
Zeichne in ein Koordinatensystem die Graphen der Funktionen Was stellst du fest? |
Meist tritt als Funktionsterm nicht nur die Quadratwurzel auf. Bei den Anwendungen sind die Funktionsterme von der Art 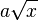 . Oft treten auch Terme von der Art
. Oft treten auch Terme von der Art 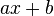 unter der Wurzel auf. Dies soll nun näher untersucht werden.
unter der Wurzel auf. Dies soll nun näher untersucht werden.
|
Du betrachstest die Funktion
|
Zurück zu Wurzelfunktion oder weiter mit Anwendungen
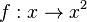 für
für  und
und 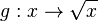 für
für 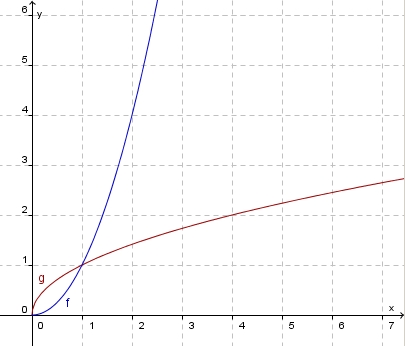
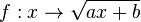 . Im folgenden Applet kannst du mit den Schiebereglern die Werte für
. Im folgenden Applet kannst du mit den Schiebereglern die Werte für  und
und 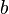 verändern. Anfangs ist
verändern. Anfangs ist 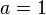 und
und 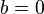 . Es ist der Graph der Quadratwurzelfunktion dargestellt.
. Es ist der Graph der Quadratwurzelfunktion dargestellt.
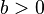 und
und 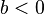 .
.
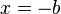 auf. Für
auf. Für 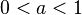 wird der Graph der Wurzelfunktion in y-Richtung gestaucht. Für
wird der Graph der Wurzelfunktion in y-Richtung gestaucht. Für 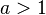 wird der Graph in y-Richtung gestreckt. Ist
wird der Graph in y-Richtung gestreckt. Ist 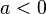 so wird der Graph mit
so wird der Graph mit  an der y-Achse gespiegelt.
an der y-Achse gespiegelt.