Wurzelfunktion Anwendungen: Unterschied zwischen den Versionen
| Zeile 62: | Zeile 62: | ||
Bei den [http://wikis.zum.de/medienvielfalt/Quadratische_Funktionen_2 quadratischen Funktionen] hast du kennengelernt, dass der Bremsweg s in m eines Autos, welches mit der Geschwindigkeit v in <math> \frac{km}{h}</math> fährt, mit der Faustregel <math> s = (\frac {v}{10})^2</math> berechnet werden kann. | Bei den [http://wikis.zum.de/medienvielfalt/Quadratische_Funktionen_2 quadratischen Funktionen] hast du kennengelernt, dass der Bremsweg s in m eines Autos, welches mit der Geschwindigkeit v in <math> \frac{km}{h}</math> fährt, mit der Faustregel <math> s = (\frac {v}{10})^2</math> berechnet werden kann. | ||
| − | Löse die Gleichung <math> s = (\frac {v}{10})^2</math> nach v auf. | + | # Löse die Gleichung <math> s = (\frac {v}{10})^2</math> nach v auf. |
| − | + | # Gib die Funktion <math>f</math> mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt. | |
| − | Gib die Funktion <math>f</math> mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt. | + | # Mit welcher Geschwindigkeit v in <math> \frac{km}{h}</math> ist wohl ein Auto, das eine Bremsspur von |
| − | + | a) 20m, <br> | |
| − | Mit welcher Geschwindigkeit v in <math> \frac{km}{h}</math> ist wohl ein Auto, das eine Bremsspur von | + | b) 40m, <br> |
| − | + | c) 60m, <br> | |
| − | + | d) 80m, <br> | |
| − | + | e) 100m <br> | |
| − | + | ||
| − | + | ||
gemacht hat, gefahren?<br> | gemacht hat, gefahren?<br> | ||
Löse graphisch und rechnerisch! | Löse graphisch und rechnerisch! | ||
| Zeile 78: | Zeile 76: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | <math> v = 10 \sqrt s</math> | + | # <math> v = 10 \sqrt s</math> |
| − | + | # <math> f: s \rightarrow 10 \sqrt s; D = R^+_0</math> | |
| − | <math> f: s \rightarrow 10 \sqrt s; D = R^+_0</math> | + | # Für die graphische Lösung kannst du in diesem Applet die entsprechenden Werte mit dem Schieberegler einstellen. |
| − | + | ||
| − | Für die graphische Lösung kannst du in diesem Applet die entsprechenden Werte mit dem Schieberegler einstellen. | + | |
<ggb_applet width="806" height="594" version="4.0" ggbBase64="UEsDBBQACAAIALpaPEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIALpaPEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVjbbtw2EH1OvmKgp6SIvaIoStpgN0GTomgAJyngtCj6RkncXca6RaT2EuTjOyQlrdZ2HOfSFohNUhzO5cyZIZ3F831ZwFa0StbV0iPnvgeiyupcVuul1+nVWeI9f/ZwsRb1WqQth1XdllwvvdBIynzpJYmY8zTzz1YJz8/CPMQjWe6fMZGmcbBiQURREvZKPq3qN7wUquGZuMw2ouQXdca1NbzRunk6m+12u/PB1HndrmfrdXq+V7kH6Galll4/eYrqTg7tqBUPfJ/M/np94dSfyUppXmXCAxNCJ589fLDYySqvd7CTud6g9yT0YCPkeoMxxUHgwcwINQhIIzItt0Lh0cnSxqzLxrNivDL7D9wMijEcD3K5lblol55/ThLGfBqNvz2oWykq3cuS3uZs0LbYSrFzas3MWkQvdV0XKTca4dMnCPzAhydmIG4IcIgit+W7bz51Q+CG0A3MyYTueOhEQycTOpmQerCVSqaFWHorXihEUFarFrM3rpU+FML60384Rk+eYExKfkRh6mPyHeT43fefmJ8If0KzMTsNkkys6rb7SqODycSP7m8y+K5A6WCTMHLTZsA+E2Z0h1EX933iJGwCLZqy/+zPDYv0rjCvW3Tr7zMYhf9JiIvZUCqLvjpAbYxszx4tSmXqhc6BzQ3tCTCsjShGljMgcxziALAagDAIGS5JApEZY6AxboRAIQEjRyjY4mAJ/gpjqywChsrM1xhrEggaCoFRILamQsBKAluXWKMBRQnGgOEhY54ERgWNIIxwRRMI0UdTkjFBQYoHcY3mA6AEqDlMYggiiIw+EppSjxLjOqoMIPIhIkYhVjVWtKtmlE+AmmiiHi5ZNZ0+gSgr82Gq62bMBUpjPzp2PdefTprig0XBU1HgPXFpMgmw5YWpCGtoVVcahiQG7tu65c1GZupSaI2nFLznW37Btdj/itJqsG1ls7pSv7e1flkXXVkpgKwu/NHnuiCTeTB6jQs62QinG2yyEU3m8a12a9yBTgm0X7dqEOd5/spIHFsDIvm2Kg4vWsGvmlqehrGY2StnIbqskLnk1Z9IVmPF4ALjDWTa1XADsSgaHKnb/PKgkMGw/1u0NV4ByTmlbM7CmAYJo2SO5w5ui4XBOSWUkjhkoR+EMbqWcVN77DwIgzjEK8j355TROZ65fSuYO8tiOyaI78UY+7qV+XT+Sr2oi3xEwgb/kje6a+3LATtja0L6uVoXwhLE9lq8lrOrtN5fOmZQp+vdocGV7+ynaws6YGMIzF257sfUjVbGODZK+VbGtxL+QDWZj/tkHlgJO6ZutFLIXedaHygZoiT+YEYq285876RoLPHNJd9VUl8MCy2zqz5S4uTfdGUqjvQxAr9I9yJxT61TK+Tfs7KYXSPh4kq0lSh6zmO6u7pTroQn5ZCLTJa4dBs9bNyk9A/0yX3NxboVvTwv7MvNgWp3/Smdb3y2qn5t6/JVtX2HfLnmwGI2eLlQWSsbw0pI8Z64Ekfm5VJxvGby6TlTpIhGZq4TBEQbtLB8O72pW/s4w66Do6nNQpT4FANtKVh1pWhlNmKv7CsPnep6v0N/yJpBHur0PfbDawmzCyuD259hKfCi2XD7OOy5yA+iPcHGantd573lXk4V5lUJpaysmpLv7XsDFaYKe6XGhzVmozo+rJ1rfa9BSfNs35sL2s4OWKlzM1nJ/QRThEl+RFrwk3CO9aKxj1/hY1XZotZ9+drJbzLPRTX6yyskkE0DtjK8X7CQ8Q4Rju3jwQbDt21jkvo+MyZH+6ZFW0ZJD3GKf6TsUdselqAGPcY9d3OdJtV9H0/+yOT5dybv7WqlhDZoB5GFmt2VWVsiykiTPjM2Qx+X3tmRdd+SAvGhckeUaxuybAqZSf0lmAHT0eO8erR/jFDjA+cnUB9ajUvvJtCrrrIVN4K5+gLYk07z/WgfAfVvp56ptfuR71twvpuwvAfygCiuHqnHX8VZ/r9wNnEkDO7H2aGbkIGzEcXnBWOMBj6lUczmP47AiOStBJ5N2759fvX/k/DsH1BLBwgBRARt8gUAAOYQAABQSwECFAAUAAgACAC6WjxA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIALpaPEABRARt8gUAAOYQAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAiQYAAAAA" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="806" height="594" version="4.0" ggbBase64="UEsDBBQACAAIALpaPEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIALpaPEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVjbbtw2EH1OvmKgp6SIvaIoStpgN0GTomgAJyngtCj6RkncXca6RaT2EuTjOyQlrdZ2HOfSFohNUhzO5cyZIZ3F831ZwFa0StbV0iPnvgeiyupcVuul1+nVWeI9f/ZwsRb1WqQth1XdllwvvdBIynzpJYmY8zTzz1YJz8/CPMQjWe6fMZGmcbBiQURREvZKPq3qN7wUquGZuMw2ouQXdca1NbzRunk6m+12u/PB1HndrmfrdXq+V7kH6Galll4/eYrqTg7tqBUPfJ/M/np94dSfyUppXmXCAxNCJ589fLDYySqvd7CTud6g9yT0YCPkeoMxxUHgwcwINQhIIzItt0Lh0cnSxqzLxrNivDL7D9wMijEcD3K5lblol55/ThLGfBqNvz2oWykq3cuS3uZs0LbYSrFzas3MWkQvdV0XKTca4dMnCPzAhydmIG4IcIgit+W7bz51Q+CG0A3MyYTueOhEQycTOpmQerCVSqaFWHorXihEUFarFrM3rpU+FML60384Rk+eYExKfkRh6mPyHeT43fefmJ8If0KzMTsNkkys6rb7SqODycSP7m8y+K5A6WCTMHLTZsA+E2Z0h1EX933iJGwCLZqy/+zPDYv0rjCvW3Tr7zMYhf9JiIvZUCqLvjpAbYxszx4tSmXqhc6BzQ3tCTCsjShGljMgcxziALAagDAIGS5JApEZY6AxboRAIQEjRyjY4mAJ/gpjqywChsrM1xhrEggaCoFRILamQsBKAluXWKMBRQnGgOEhY54ERgWNIIxwRRMI0UdTkjFBQYoHcY3mA6AEqDlMYggiiIw+EppSjxLjOqoMIPIhIkYhVjVWtKtmlE+AmmiiHi5ZNZ0+gSgr82Gq62bMBUpjPzp2PdefTprig0XBU1HgPXFpMgmw5YWpCGtoVVcahiQG7tu65c1GZupSaI2nFLznW37Btdj/itJqsG1ls7pSv7e1flkXXVkpgKwu/NHnuiCTeTB6jQs62QinG2yyEU3m8a12a9yBTgm0X7dqEOd5/spIHFsDIvm2Kg4vWsGvmlqehrGY2StnIbqskLnk1Z9IVmPF4ALjDWTa1XADsSgaHKnb/PKgkMGw/1u0NV4ByTmlbM7CmAYJo2SO5w5ui4XBOSWUkjhkoR+EMbqWcVN77DwIgzjEK8j355TROZ65fSuYO8tiOyaI78UY+7qV+XT+Sr2oi3xEwgb/kje6a+3LATtja0L6uVoXwhLE9lq8lrOrtN5fOmZQp+vdocGV7+ynaws6YGMIzF257sfUjVbGODZK+VbGtxL+QDWZj/tkHlgJO6ZutFLIXedaHygZoiT+YEYq285876RoLPHNJd9VUl8MCy2zqz5S4uTfdGUqjvQxAr9I9yJxT61TK+Tfs7KYXSPh4kq0lSh6zmO6u7pTroQn5ZCLTJa4dBs9bNyk9A/0yX3NxboVvTwv7MvNgWp3/Smdb3y2qn5t6/JVtX2HfLnmwGI2eLlQWSsbw0pI8Z64Ekfm5VJxvGby6TlTpIhGZq4TBEQbtLB8O72pW/s4w66Do6nNQpT4FANtKVh1pWhlNmKv7CsPnep6v0N/yJpBHur0PfbDawmzCyuD259hKfCi2XD7OOy5yA+iPcHGantd573lXk4V5lUJpaysmpLv7XsDFaYKe6XGhzVmozo+rJ1rfa9BSfNs35sL2s4OWKlzM1nJ/QRThEl+RFrwk3CO9aKxj1/hY1XZotZ9+drJbzLPRTX6yyskkE0DtjK8X7CQ8Q4Rju3jwQbDt21jkvo+MyZH+6ZFW0ZJD3GKf6TsUdselqAGPcY9d3OdJtV9H0/+yOT5dybv7WqlhDZoB5GFmt2VWVsiykiTPjM2Qx+X3tmRdd+SAvGhckeUaxuybAqZSf0lmAHT0eO8erR/jFDjA+cnUB9ajUvvJtCrrrIVN4K5+gLYk07z/WgfAfVvp56ptfuR71twvpuwvAfygCiuHqnHX8VZ/r9wNnEkDO7H2aGbkIGzEcXnBWOMBj6lUczmP47AiOStBJ5N2759fvX/k/DsH1BLBwgBRARt8gUAAOYQAABQSwECFAAUAAgACAC6WjxA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIALpaPEABRARt8gUAAOYQAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAiQYAAAAA" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| − | + | a) 44,7 <math> \frac{km}{h}</math><br> | |
| − | + | b) 63,2 <math> \frac{km}{h}</math><br> | |
| − | + | c) 77,5 <math> \frac{km}{h}</math><br> | |
| − | + | d) 89,4 <math> \frac{km}{h}</math><br> | |
| − | + | e) 100 <math> \frac{km}{h}</math><br> | |
}} | }} | ||
Version vom 29. Januar 2012, 10:10 Uhr
Viele Anwendungen der Wurzelfunktion haben einen Faktor a. Daher wird zuerst die Funktion 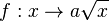 betrachtet.
betrachtet.
|
Im Applet ist der Graph der Wurzelfunktion Wie ändert sich der Graph der Wurzelfunktion
|
- Für a = -1 wird der Graph der Wurzelfunktion
 an der x-Achse gespiegelt.
an der x-Achse gespiegelt.
- Für 0 < a < 1 wird der Graph der Wurzelfunktion
 in y-Richtung gestaucht.
in y-Richtung gestaucht.
- Für 1 < a wir der Graph der Wurzelfunktion
 in y-Richtung gestreckt.
in y-Richtung gestreckt.
- Für negative a wird der Graph von 2. oder 3. an der y-Achse gespiegelt.
|
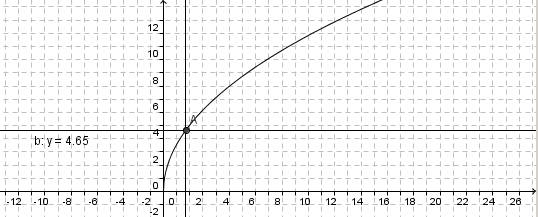
Gib die Funktion, die jeder Oberfläche eines Würfels die Kantenlänge zuordnet als Funktionsterm an.
|
|
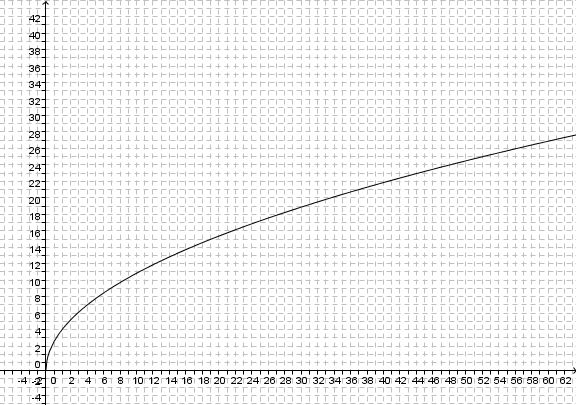
Schau dir diesen Video an. Die Erde kann näherungsweise als Kugel angesehen werden. Die Sichtweite auf der Erde kann man bei guten Bedingungen durch die Formel
|
|
Bei den quadratischen Funktionen hast du kennengelernt, dass der Bremsweg s in m eines Autos, welches mit der Geschwindigkeit v in
a) 20m, |
-
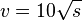
-
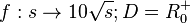
- Für die graphische Lösung kannst du in diesem Applet die entsprechenden Werte mit dem Schieberegler einstellen.
a) 44,7 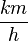
b) 63,2 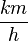
c) 77,5 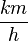
d) 89,4 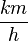
e) 100 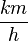
Zurück zu Wurzelfunktion oder weiter mit Übungen.
 dargestellt.
dargestellt.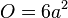
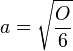
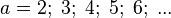
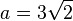
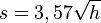 (vgl.
(vgl. 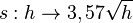 .
.

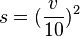 berechnet werden kann.
berechnet werden kann.
 mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.
mit Defintionsmenge an, die den Zusammenhang Bremsweg --> Geschwindigkeit beschreibt.

