Wurzelfunktion allgemeine Wurzelfunktion: Unterschied zwischen den Versionen
| Zeile 49: | Zeile 49: | ||
<math> f: x \rightarrow \sqrt[n]{x}\</math> mit <math> x \in R^+_0</math> und <math>n \in N</math>. | <math> f: x \rightarrow \sqrt[n]{x}\</math> mit <math> x \in R^+_0</math> und <math>n \in N</math>. | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Aufgabe|Gib für die Würfelaufgabe die zugehörige Funktion an.}} | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | <math>f:V \rightarrow \sqrt[3]{V}</math> mit <math>V \in R^+_0</math> | ||
}} | }} | ||
Version vom 30. Januar 2012, 08:44 Uhr
Ein Würfel mit Seitenlänge a hat dasVolumen 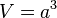 .
.
Man weiß von einem Würfel, dass es das Volumen 27 VE hat. Wie lang ist dann die Seite? Natürlich 3 LE.
Es ist
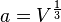
Man schreibt auch dafür
|
Merke:
Die Gleichung 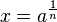 oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\ oder Fehler beim Parsen(Lexikalischer Fehler): x = \sqrt[n]{a}\
Fehler beim Parsen(Lexikalischer Fehler): \sqrt[n]{a}\ heißt die n-te Wurzel aus a. |
|
a) Setze verschiedene Werte für das Würfelvolumen V ein, und berechne welche Werte sich für die Seitenlänge a ergeben. Trage die Ergebnisse in eine Wertetabelle ein. b) Erstelle ein V-a-Diagramm (V nach rechts, a nach oben antragen!) |
|
Merke:
Man definiert für jede natürliche Zahl n die allgemeine Wurzelfunktion n-ten Grades oder n-te Wurzelfunktion Fehler beim Parsen(Lexikalischer Fehler): f: x \rightarrow \sqrt[n]{x}\ mit |
|
Gib für die Würfelaufgabe die zugehörige Funktion an. |
![f:V \rightarrow \sqrt[3]{V}](/images/math/5/6/2/56277ceb06d9f1e85ce77b321e54ee46.png) mit
mit 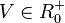


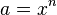 hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung
hat für jede natürliche Zahl n und jede nicht negative reelle Zahl x als Lösung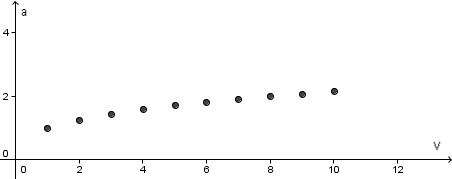
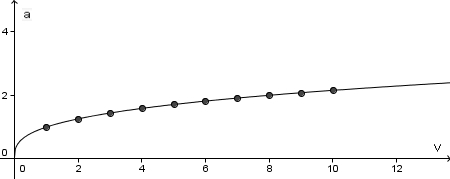
 und
und 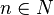 .
.

