Rationale Funktionen Einführung: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | Astronauten, die von einer Raumstation,welche in der Höhe | + | Astronauten, die von einer Raumstation,welche in der Höhe x um die Erde kreist, auf die Erde blicken, sehen eine Kugelhaube. |
<center>[[Datei:Erde_tangenten.jpg|300px]]</center> | <center>[[Datei:Erde_tangenten.jpg|300px]]</center> | ||
| Zeile 5: | Zeile 5: | ||
{{Aufgabe| | {{Aufgabe| | ||
| − | Die Mantelfläche <math>M</math> der Kugelhaube ist <math>M = 2\pi R | + | Die Mantelfläche <math>M</math> der Kugelhaube ist <math>M = 2\pi R h</math> wobei <math>R</math> der Erdradius 6370km und <math>l</math> die Länge der Strecke [CD] ist. |
| − | 1. Zeige, dass die Mantelfläche <math>M</math> in Abhängigkeit der Höhe h zu <math>M=\frac{2\pi R^2h}{R+ | + | 1. Zeige, dass die Mantelfläche <math>M</math> in Abhängigkeit der Höhe h zu <math>M=\frac{2\pi R^2h}{R+x}</math> ergibt. |
| − | Die Höhe <math> | + | Die Höhe <math>x</math> ist die Variable für die Mantelfläche <math>M</math>. |
2. a) Bestimme die Definitionsmenge. | 2. a) Bestimme die Definitionsmenge. | ||
| − | b) Welchen Wert dürftest du nicht für | + | b) Welchen Wert dürftest du nicht für x einsetzen? |
| − | c) Welcher Grenzwert ergibt sich für die Mantelfläche <math> M</math> für <math> | + | c) Welcher Grenzwert ergibt sich für die Mantelfläche <math> M</math> für <math> x \rightarrow \infty</math>? |
}} | }} | ||
| Zeile 24: | Zeile 24: | ||
In diesem Bild betrachet man die zwei rechtwinkligen Dreiecke <math>\Delta AMS</math> und <math> \Delta AMD</math>, welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich: | In diesem Bild betrachet man die zwei rechtwinkligen Dreiecke <math>\Delta AMS</math> und <math> \Delta AMD</math>, welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich: | ||
| − | Im Dreieck <math>\Delta AMS</math> betrachtet man das Streckenverhältnis <math>\frac {\bar {SM}}{\bar {}{MA}} = \frac {R+ | + | Im Dreieck <math>\Delta AMS</math> betrachtet man das Streckenverhältnis <math>\frac {\bar {SM}}{\bar {}{MA}} = \frac {R+x}{R}</math>. Das entsprechende Seitenverhältnis im Dreieck <math> \Delta AMD</math> ist <math>\frac {\bar {MA}}{\bar {}{MD}} = \frac {R}{R-h}</math>. |
| − | Also ist <math>\frac {R+ | + | Also ist <math>\frac {R+x}{R} = \frac {R}{R-h}</math>. |
| − | Formt man um <math> R- | + | Formt man um <math> R-h = \frac{R^2}{R+x}</math> und löst nach h auf und fasst die rechte Seite zusammen, dann ergibt sich <math> h = R - \frac{R^2}{R+x}=\frac{R^2+Rx-R^2}{R+x}=\frac{Rh}{R+x}</math>. |
| − | Setzt man den Term für | + | Setzt man den Term für h in die Formel für die Mantelfläche ein, so ergibt sich <math> M = \frac {2 \pi R^2 x}{R+x}</math> |
2. a) <math> D = [0;\infty[</math> | 2. a) <math> D = [0;\infty[</math> | ||
| − | b) <math> | + | b) <math> x \not= -R</math> |
c) <math> M = 2 \pi R^2</math> | c) <math> M = 2 \pi R^2</math> | ||
}} | }} | ||
Version vom 9. Februar 2013, 14:58 Uhr
Astronauten, die von einer Raumstation,welche in der Höhe x um die Erde kreist, auf die Erde blicken, sehen eine Kugelhaube.
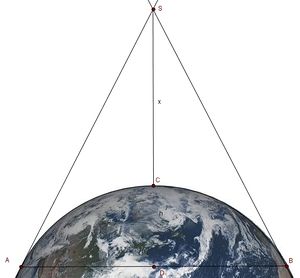
|
Die Mantelfläche 1. Zeige, dass die Mantelfläche Die Höhe 2. a) Bestimme die Definitionsmenge. b) Welchen Wert dürftest du nicht für x einsetzen? c) Welcher Grenzwert ergibt sich für die Mantelfläche
|
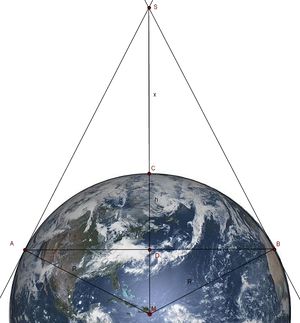
In diesem Bild betrachet man die zwei rechtwinkligen Dreiecke 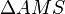 und
und 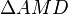 , welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich:
Im Dreieck
, welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich:
Im Dreieck 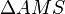 betrachtet man das Streckenverhältnis
betrachtet man das Streckenverhältnis 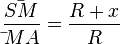 . Das entsprechende Seitenverhältnis im Dreieck
. Das entsprechende Seitenverhältnis im Dreieck 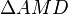 ist
ist 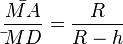 .
.
Also ist 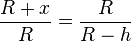 .
.
Formt man um 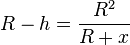 und löst nach h auf und fasst die rechte Seite zusammen, dann ergibt sich
und löst nach h auf und fasst die rechte Seite zusammen, dann ergibt sich 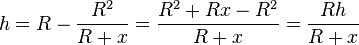 .
.
Setzt man den Term für h in die Formel für die Mantelfläche ein, so ergibt sich 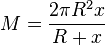
2. a) 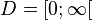
b) 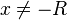
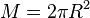
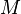 der Kugelhaube ist
der Kugelhaube ist 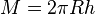 wobei
wobei 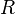 der Erdradius 6370km und
der Erdradius 6370km und 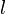 die Länge der Strecke [CD] ist.
die Länge der Strecke [CD] ist.
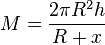 ergibt.
ergibt.
 ist die Variable für die Mantelfläche
ist die Variable für die Mantelfläche 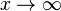 ?
?

