Rationale Funktionen Einführung: Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
{{Aufgabe| | {{Aufgabe| | ||
| − | Die Mantelfläche <math>M</math> der Kugelhaube ist <math>M = 2\pi R h</math> wobei <math>R</math> der Erdradius | + | Die Mantelfläche <math>M</math> der Kugelhaube ist <math>M = 2\pi R h</math> wobei <math>R</math> der Erdradius <math>R = 6370 km</math> und <math>h</math> die Länge der Strecke [CD] ist. |
| − | 1. Zeige, dass die Mantelfläche <math>M</math> in Abhängigkeit der Höhe | + | 1. Zeige, dass die Mantelfläche <math>M</math> in Abhängigkeit der Höhe <math>x</math> sich zu <math>M=\frac{2\pi R^2h}{R+x}</math> ergibt. |
Die Höhe <math>x</math> ist die Variable für die Mantelfläche <math>M</math>. | Die Höhe <math>x</math> ist die Variable für die Mantelfläche <math>M</math>. | ||
Version vom 9. Februar 2013, 15:00 Uhr
Astronauten, die von einer Raumstation,welche in der Höhe x um die Erde kreist, auf die Erde blicken, sehen eine Kugelhaube.
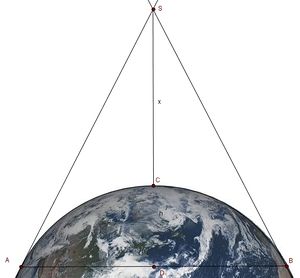
|
Die Mantelfläche 1. Zeige, dass die Mantelfläche Die Höhe 2. a) Bestimme die Definitionsmenge. b) Welchen Wert dürftest du nicht für x einsetzen? c) Welcher Grenzwert ergibt sich für die Mantelfläche
|
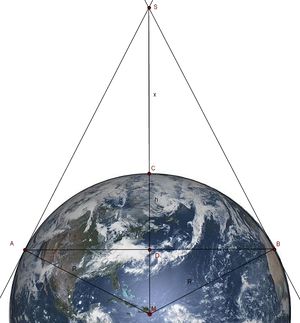
In diesem Bild betrachet man die zwei rechtwinkligen Dreiecke 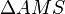 und
und 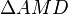 , welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich:
Im Dreieck
, welche zueinander ähnlich sind. In ähnlichen Dreiecken sind die Streckenverhältnisse entsprechender Seiten gleich:
Im Dreieck 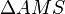 betrachtet man das Streckenverhältnis
betrachtet man das Streckenverhältnis 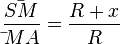 . Das entsprechende Seitenverhältnis im Dreieck
. Das entsprechende Seitenverhältnis im Dreieck 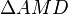 ist
ist 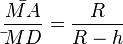 .
.
Also ist 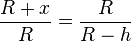 .
.
Formt man um 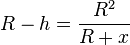 und löst nach h auf und fasst die rechte Seite zusammen, dann ergibt sich
und löst nach h auf und fasst die rechte Seite zusammen, dann ergibt sich 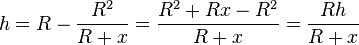 .
.
Setzt man den Term für h in die Formel für die Mantelfläche ein, so ergibt sich 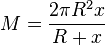
2. a) 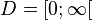
b) 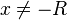
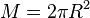
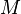 der Kugelhaube ist
der Kugelhaube ist 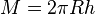 wobei
wobei 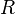 der Erdradius
der Erdradius 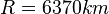 und
und 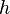 die Länge der Strecke [CD] ist.
die Länge der Strecke [CD] ist.
 sich zu
sich zu 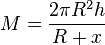 ergibt.
ergibt.
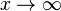 ?
?

