Rationale Funktionen Definitionsmenge: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 37: | Zeile 37: | ||
|- | |- | ||
| <math>f(x) = \frac{x^2-2x}{x^2-64}</math> || D = R \{-8;8} | | <math>f(x) = \frac{x^2-2x}{x^2-64}</math> || D = R \{-8;8} | ||
| + | |- | ||
| + | | <math>f(x) = \frac{x^2-2x}{x^2+64}</math> || D = R | ||
|} | |} | ||
</div> | </div> | ||
Version vom 23. Februar 2013, 09:43 Uhr
|
Der Nenner eines Bruches darf nie den Wert Null annehmen darf. Daher darf man für Die Nullstellen des Nennerpolynoms werden als Definitionslücken bezeichnet. Die Definitionsmenge der gebrochen-rationalen Funktion
|
Beispiele:
Die Funktion
1. 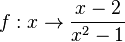 hat, da sich der Nenner
hat, da sich der Nenner 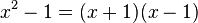 umformen lässt, die Definitionslücken
umformen lässt, die Definitionslücken 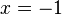 und
und 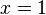 , also ist
, also ist 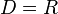 \
\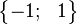 .
.
2. 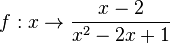 hat, da sich der Nenner
hat, da sich der Nenner 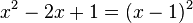 umformen lässt, die Definitionslücke
umformen lässt, die Definitionslücke 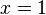 , also ist
, also ist 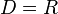 \
\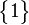 .
.
3. 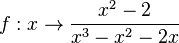 hat, da sich der Nenner
hat, da sich der Nenner 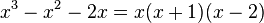 umformen lässt, die Definitionslücken
umformen lässt, die Definitionslücken 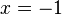 ,
,  und
und 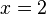 , also ist
, also ist 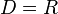 \
\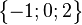 .
.
|
Ordne die Definitionsmengen und die angegebenen Funktionen |
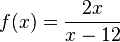 |
D = R \{12} |
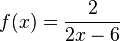 |
D = R \{3} |
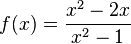 |
D = R \{-1;1} |
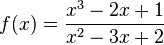 |
D = R \{1;2} |
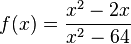 |
D = R \{-8;8} |
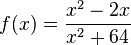 |
D = R |
 keine Werte einsetzen, dass das Nennerpolynom
keine Werte einsetzen, dass das Nennerpolynom 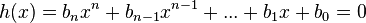 ist.
ist.
 mit
mit 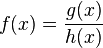 ist die Menge der reellen Zahlen ohne die Nullstellen des Nennerpolynoms h(x).
ist die Menge der reellen Zahlen ohne die Nullstellen des Nennerpolynoms h(x).
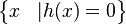
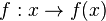 richtig zu!
richtig zu!

