Rationale Funktionen Polstellen: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 1: | Zeile 1: | ||
Die Funktion <math>f: x \rightarrow \frac{1}{x}</math> ist für <math> x = 0 </math> nicht definiert. Wie verhält sie sich in der Umgebung von <math>0</math>? Je kleiner <math>x</math> betragsmäßig wird, desto größer wird der Betrag von <math>\frac{1}{x}</math>. Der Graph von <math>f</math> sieht so aus: | Die Funktion <math>f: x \rightarrow \frac{1}{x}</math> ist für <math> x = 0 </math> nicht definiert. Wie verhält sie sich in der Umgebung von <math>0</math>? Je kleiner <math>x</math> betragsmäßig wird, desto größer wird der Betrag von <math>\frac{1}{x}</math>. Der Graph von <math>f</math> sieht so aus: | ||
| − | <center>[[ | + | <center>[[Bild:Indirekte_proportionalität.jpg]]</center> |
| + | |||
| + | Zeigt eine Funktion für einen x-Wert ein solches Verhalten, dann ist der x-Wert eine Definitionslücke und man bezeichnet diese Stelle als Polstelle. | ||
{{Merke|Ist an einer Definitionslücke <math>x_0</math> einer gebrochen-rationalen Funktion <math>f</math> | {{Merke|Ist an einer Definitionslücke <math>x_0</math> einer gebrochen-rationalen Funktion <math>f</math> | ||
Version vom 27. Februar 2013, 15:26 Uhr
Die Funktion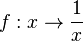 
ist für 
nicht definiert. Wie verhält sie sich in der Umgebung von 
? Je kleiner 
betragsmäßig wird, desto größer wird der Betrag von 
. Der Graph von 
sieht so aus:
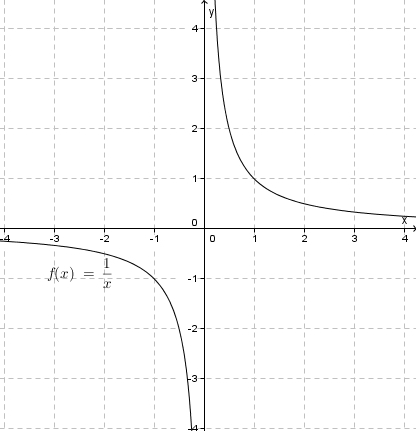
Zeigt eine Funktion für einen x-Wert ein solches Verhalten, dann ist der x-Wert eine Definitionslücke und man bezeichnet diese Stelle als Polstelle.
 Merke
Ist an einer Definitionslücke
dann ist die Definitionslücke |
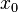einer gebrochen-rationalen Funktion 
,
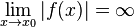