Rationale Funktionen Polstellen: Unterschied zwischen den Versionen
| Zeile 41: | Zeile 41: | ||
e) <math>l</math> mit <math> l(x) = \frac{1}{(x-3)(x+2)}</math> | e) <math>l</math> mit <math> l(x) = \frac{1}{(x-3)(x+2)}</math> | ||
| − | f) <math>m</math> mit <math> m(x) = \frac{1}{(x-3)}+\frac{1}{x}</math> | + | f) <math>m</math> mit <math> m(x) = \frac{1}{(x-3)}+ \frac{1}{x}</math> |
}} | }} | ||
Version vom 5. April 2013, 13:27 Uhr
Die Funktion 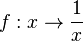 ist für
ist für  nicht definiert. Wie verhält sie sich in der Umgebung von
nicht definiert. Wie verhält sie sich in der Umgebung von  ? Je kleiner
? Je kleiner  betragsmäßig wird, desto größer wird der Betrag von
betragsmäßig wird, desto größer wird der Betrag von  . Zeigt eine Funktion für einen x-Wert ein solches Verhalten, dann ist der x-Wert eine Definitionslücke und man bezeichnet diese Stelle als Polstelle.
. Zeigt eine Funktion für einen x-Wert ein solches Verhalten, dann ist der x-Wert eine Definitionslücke und man bezeichnet diese Stelle als Polstelle.
|
Ist an einer Definitionslücke
dann ist die Definitionslücke |
Beispiele:
1. Die Funktion 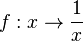 hat für
hat für  einen Pol 1. Ordnung (
einen Pol 1. Ordnung ( ist einfache Nullstelle des Nenners).
ist einfache Nullstelle des Nenners).
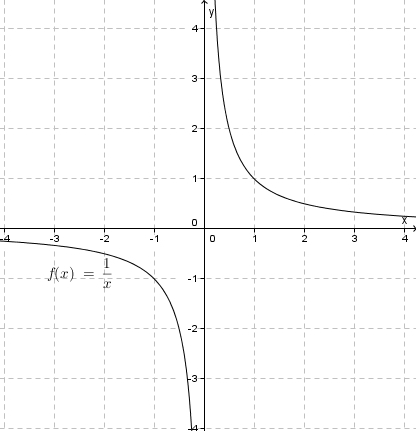
Nähert man sich von links an, also 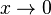 mit
mit 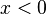 , dann streben die Funktionswerte nach
, dann streben die Funktionswerte nach 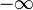 ; nähert man sich von rechts an, also
; nähert man sich von rechts an, also 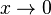 mit
mit 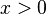 , dann streben die Funktionswerte nach
, dann streben die Funktionswerte nach 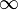 .
.  hat an
hat an  eine Polstelle mit Vorzeichenwechsel. Die Gerade
eine Polstelle mit Vorzeichenwechsel. Die Gerade  ist senkrechte Asymptote des Graphen von
ist senkrechte Asymptote des Graphen von  .
.
2. Die Funktion 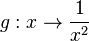 hat für
hat für  einen Pol 2. Ordnung (
einen Pol 2. Ordnung ( ist zweifache Nullstelle des Nenners).
ist zweifache Nullstelle des Nenners).
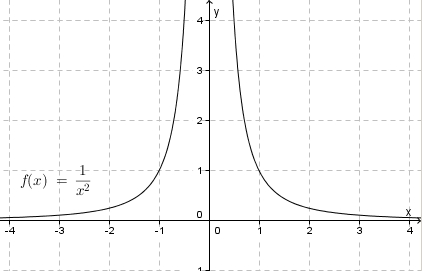
Nähert man sich von links oder von rechts an, also 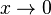 mit
mit 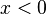 oder
oder 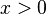 , dann streben die Funktionswerte in beiden Fällen nach
, dann streben die Funktionswerte in beiden Fällen nach 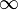 .
. 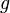 hat an
hat an  eine Polstelle ohne Vorzeichenwechsel. Die Gerade
eine Polstelle ohne Vorzeichenwechsel. Die Gerade  ist senkrechte Asymptote des Graphen von
ist senkrechte Asymptote des Graphen von  .
.
|
Man kann allgemein für eine gebrochen-rationale Funktion Ist n gerade, dann hat die Funktion Ist n ungerade, dann hat die Funktion Die Ordnung der Polstelle |
|
Ermittle bei den gegebenen Funktionen jeweils die Polstelle(n) der Funktion und beschreibe das Vorzeichenverhalten der Funktion bei Annäherung an die Polstelle(n). a) b) c) d) e) f) |
a) x = 2; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<2): 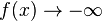 ; Annäherung von rechts (x>2):
; Annäherung von rechts (x>2): 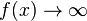
b) x = 2; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<2): 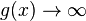 ; Annäherung von rechts (x>2):
; Annäherung von rechts (x>2): 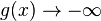
c) x = 2; Pol 2. Ordnung; Pol ohne Vorzeichenwechsel; Annäherung von links (x<2): 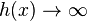 ; Annäherung von rechts (x>2):
; Annäherung von rechts (x>2): 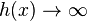
d) x = 3; Pol 7. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<3): 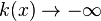 ; Annäherung von rechts (x>3):
; Annäherung von rechts (x>3): 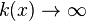
e) x = -2; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<-2): 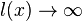 ; Annäherung von rechts (x>-2):
; Annäherung von rechts (x>-2): 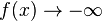
- x = 3; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<3):
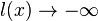 ; Annäherung von rechts (x>3):
; Annäherung von rechts (x>3): 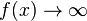
e) x = 0; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<-2): 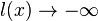 ; Annäherung von rechts (x>-2):
; Annäherung von rechts (x>-2): 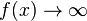
- x = 3; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<3):
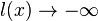 ; Annäherung von rechts (x>3):
; Annäherung von rechts (x>3): 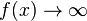
|
Ordne die Polstellen und die angegebenen Funktionen |
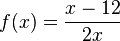 |

|
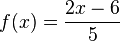 |
keine Polstelle |
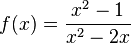 |
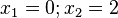
|
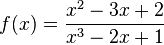 |
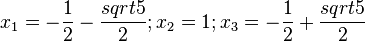
|
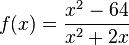 |
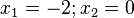
|
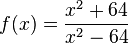 |
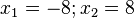
|
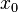 einer gebrochen-rationalen Funktion
einer gebrochen-rationalen Funktion 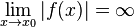 ,
,
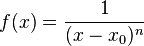 formulieren:
formulieren:
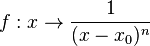 mit
mit 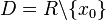 an der Stelle
an der Stelle 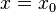 einen Pol ohne Vorzeichenwechsel.
einen Pol ohne Vorzeichenwechsel.
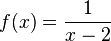
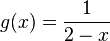
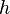 mit
mit 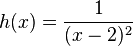
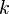 mit
mit 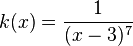
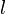 mit
mit 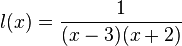
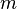 mit
mit 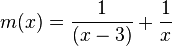
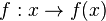 richtig zu!
richtig zu!

