Rationale Funktionen Polstellen: Unterschied zwischen den Versionen
| Zeile 81: | Zeile 81: | ||
Beschreibe, was du mit dem Schieberegler für <math>x_0</math> ändern kannst. | Beschreibe, was du mit dem Schieberegler für <math>x_0</math> ändern kannst. | ||
}} | }} | ||
| − | + | <center> | |
| − | <ggb_applet width="532" height="492" version="5.0" ggbBase64=" | + | <ggb_applet width="532" height="492" version="5.0" ggbBase64="UEsDBBQACAgIAP11hkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAP11hkIAAAAAAAAAAAAAAAASAAAAZ2VvZ2VicmFfcHl0aG9uLnB5AwBQSwcIAAAAAAIAAAAAAAAAUEsDBBQACAgIAP11hkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVhtb9s2EP6c/gpCn1ogtkmRku3CbtEXFCuQdsXSDcM+bKAl2mYjS4JEvwX98TseKVl2kyxJi2JBFL4d73jPHR+SmbzcrTKyUVWti3wasD4NiMqTItX5Yhqszbw3Cl6+eDJZqGKhZpUk86JaSTMNIivZzhP9cZ+xoe3TKagZJZRHsepF45D2RBipnlQj2pNzKnkUCiVGMiBkV+vnefFRrlRdykRdJku1khdFIg0qXRpTPh8MttttvzHfL6rFYLGY9Xd1GhBYel5PA195DuqOJm05ioeUssGfHy6c+p7OayPzRAXEurXWL56cTbY6T4st2erULME1AW4slV4swc84hMbACpXgbKkSozeqhqmdJvpsVmWAYjK342euRrLWnYCkeqNTVVmYx/z4JyBFpVVuvCzzNgeNtslGq61Ta2tocRQQUxTZTFqN4CT5SqAIXcEJ+YqVyLWFb8auOcSCUd87sn/GthFDVHWtZ5maBnOZ1YCTzucVxKht12afKbTqOw4+snPwpNbXIMwpAOeAxeWd2y+GT1CPaMcV1rFqqvWdRt34wWZrMeLh/S2KDniIQkhDSs5twVwRQhHHboi6PkAVi9AVwhWRkxFuunCiwskIJyP498HauBg+BNTwu2weAjm6wWYY3RLIu/LHRe4+frKoYxNM4S9+31jkd7l5avE0dx5jMBY/20VBx8Mf7iQP43MWD89jcbPRIf3JuLKYj+6C9gHb5AFWIxaeMgEjEez3iLCxZYAh/BlaUg0Jg76RbUJLEI6ylk+jCMQjSpil4BhpNAJqjbANBuBD4Yhz+Cw/RFzAZ7VGQDdRiHZ5DCN8RMSYRDH0EI6UPsSpwC72lxGBs+hDsv7xQE0Gzbkz8RiRemllPUkbtaotahyWPD5gh6B5AA/YiQiaAGAcIYa8gXFErBxAhGQZWYTF0IMLyMa2d0jxwCKImwUaWFUQYFaCPA0ghhwjAdCRyJoH2B2mogOrpeihRZXDRGiD+dDCzLlDOoxJHJKhpXkmLPvHI7t60BoSCEnMrM42DmAXpowItw4B8ZVFrVuAlyorG5wQSp2Xa3MEX7JKm6opyjZOKJ0WydXrFm4/omRtumJwPzjcQtx94eiScjbJ5ExlcJe7tMlAyEZmltnRwrzIDWnyIHR9i0qWS53Ul8oYmFWTL3IjL6RRu3cgXTe20TTenSZqnWQ61TL/AxLFqrAKSXuVsuzcXKUEMCdaSYqiSi/3NWQP2f2lqgLOKjbqDylnoRjjzwjg3PuhIeuL4ZjF/sceTIm0ec95v3uHCnHS7WNoW21a3+RO1Q3+i0qn3fr7+nWRpS3WZaFz80aWZl3hxRjWUFmnXuWLTCG2eNzCDTO5mhW7Swcqd7o+70toUWd/tnhTZEVFYFuGUQQCvpy5EmXswlopijIUJWgTJZ2242wcogSWM1eiFITdLc07yhovGW3M6Bo5EJR30xJzZhrsArLOtblwLUhRnVx5V5mb8HG9mkG+tTkMAm+1u127p8SxGXajmf0PMTMZnCTi5EpVucpcuuUQ8HWxrl3+tzl8NlnX6pM0y1d5+ptawM79JC2DGrDmRNGi248q0SuY6Po9xNKG/3dYvetN1aJSXl5m+GBxAcBR2k3+b7pR1buqWL3PN58ht06WOhk0/kzqpNKlzWAyA0a/UocsTXUt4UBIu/OOYOFvb9l+1L7c9p36tav3WD9qt1uEIzvMeXsVRTnf6sX0m3g/OK3oTfH+zhy6h87wRp3Xj9FZZsCVR5zdbtiujXszAcSuLG2oIVEPN6DukeD525uvii+W/IucmAPpnOwNmwR2T9SwFC+rjXUrIHJtlkWFT1XwA0qbQJlawcPUK8zXK1Xp5BDNfyi+eiFb1z6h241v10mKmV3RCbYHEGD4FqYjMiuX0qajdy6Te1Ud7RnU9qFIG8PebGYf2WSl4RzuAQWv5A5yF/TN6iJbG3WZwCbND/9mcCvzBxa8bTDJ7fsV98Q0GGNlrnednQYo6WuglWOOODCugUP0Cl7uNWZXEwus/KLTVOXtamUOtIJRgP1YWnfthiuVcsneToXM2uPR06EEH5r/DFJ+GiL+PwoR8xFi9PEhin5qiNhjArQrK7BllXiA53Cd29lL39PdMzKFi/OAPN2RHoEd9ezvp/kzd8E7Dux8neOODQ5KHhPFkIpb4kjvjOOv83mtDCIfI+49Ie4KMwbk9CC9MQL8rgh0cRx0iQtvof4/gy/+BVBLBwig/sichQYAAMoUAABQSwECFAAUAAgICAD9dYZC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAP11hkIAAAAAAgAAAAAAAAASAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYV9weXRob24ucHlQSwECFAAUAAgICAD9dYZCoP7InIUGAADKFAAADAAAAAAAAAAAAAAAAACfAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAvgAAAF4HAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> |
| − | + | </center> | |
{{Merke|Man kann allgemein für eine gebrochen-rationale Funktion <math> f</math> mit <math> f(x)=\frac{1}{(x-x_0)^n}</math> formulieren: | {{Merke|Man kann allgemein für eine gebrochen-rationale Funktion <math> f</math> mit <math> f(x)=\frac{1}{(x-x_0)^n}</math> formulieren: | ||
Version vom 6. April 2013, 13:49 Uhr
Die Funktion 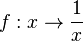 ist für
ist für  nicht definiert. Wie verhält sie sich in der Umgebung von
nicht definiert. Wie verhält sie sich in der Umgebung von  ? Je kleiner
? Je kleiner  betragsmäßig wird, desto größer wird der Betrag von
betragsmäßig wird, desto größer wird der Betrag von  . Zeigt eine Funktion für einen x-Wert ein solches Verhalten, dann ist der x-Wert eine Definitionslücke und man bezeichnet diese Stelle als Polstelle.
. Zeigt eine Funktion für einen x-Wert ein solches Verhalten, dann ist der x-Wert eine Definitionslücke und man bezeichnet diese Stelle als Polstelle.
|
Ist an einer Definitionslücke
dann ist die Definitionslücke |
Beispiele:
1. Die Funktion 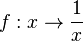 hat für
hat für  einen Pol 1. Ordnung (
einen Pol 1. Ordnung ( ist einfache Nullstelle des Nenners).
ist einfache Nullstelle des Nenners).
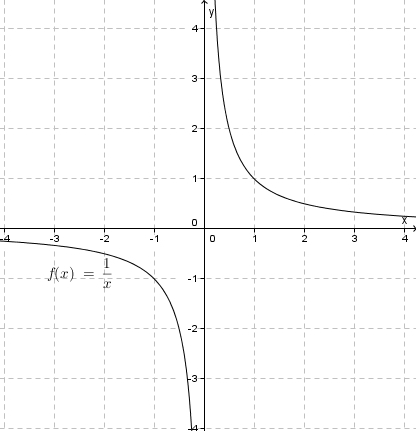
Nähert man sich von links an, also 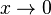 mit
mit 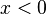 , dann streben die Funktionswerte nach
, dann streben die Funktionswerte nach 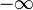 ; nähert man sich von rechts an, also
; nähert man sich von rechts an, also 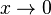 mit
mit 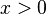 , dann streben die Funktionswerte nach
, dann streben die Funktionswerte nach 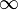 .
.  hat an
hat an  eine Polstelle mit Vorzeichenwechsel. Die Gerade
eine Polstelle mit Vorzeichenwechsel. Die Gerade  ist senkrechte Asymptote des Graphen von
ist senkrechte Asymptote des Graphen von  .
.
2. Die Funktion 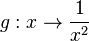 hat für
hat für  einen Pol 2. Ordnung (
einen Pol 2. Ordnung ( ist zweifache Nullstelle des Nenners).
ist zweifache Nullstelle des Nenners).
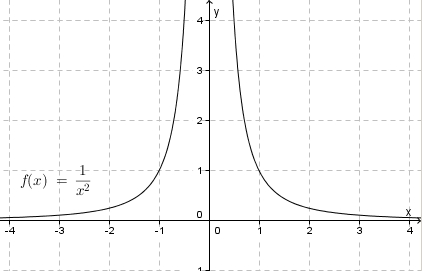
Nähert man sich von links oder von rechts an, also 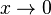 mit
mit 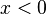 oder
oder 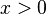 , dann streben die Funktionswerte in beiden Fällen nach
, dann streben die Funktionswerte in beiden Fällen nach 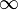 .
. 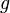 hat an
hat an  eine Polstelle ohne Vorzeichenwechsel. Die Gerade
eine Polstelle ohne Vorzeichenwechsel. Die Gerade  ist senkrechte Asymptote des Graphen von
ist senkrechte Asymptote des Graphen von  .
.
|
Ermittle bei den gegebenen Funktionen jeweils die Polstelle(n) der Funktion und beschreibe das Vorzeichenverhalten der Funktion bei Annäherung an die Polstelle(n). a) b) c) d) e) f) |
a) x = 2; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<2): 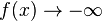 ; Annäherung von rechts (x>2):
; Annäherung von rechts (x>2): 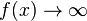
b) x = 2; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<2): 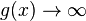 ; Annäherung von rechts (x>2):
; Annäherung von rechts (x>2): 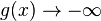
c) x = 2; Pol 2. Ordnung; Pol ohne Vorzeichenwechsel; Annäherung von links (x<2): 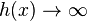 ; Annäherung von rechts (x>2):
; Annäherung von rechts (x>2): 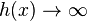
d) x = 3; Pol 7. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<3): 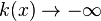 ; Annäherung von rechts (x>3):
; Annäherung von rechts (x>3): 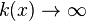
e) x = -2; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<-2): 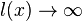 ; Annäherung von rechts (x>-2):
; Annäherung von rechts (x>-2): 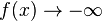
- x = 3; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<3):
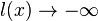 ; Annäherung von rechts (x>3):
; Annäherung von rechts (x>3): 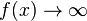
e) x = 0; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<-2): 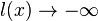 ; Annäherung von rechts (x>-2):
; Annäherung von rechts (x>-2): 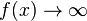
- x = 3; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<3):
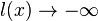 ; Annäherung von rechts (x>3):
; Annäherung von rechts (x>3): 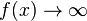
|
Ordne die Polstellen und die angegebenen Funktionen |
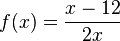 |

|
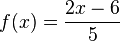 |
keine Polstelle |
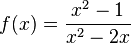 |
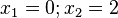
|
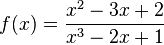 |
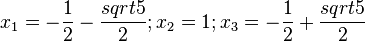
|
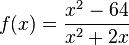 |
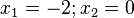
|
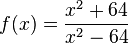 |
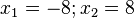
|
|
Im folgenden Applet kannst du mit dem Schieberegler die Potenz n des Nenners der Funktion Beschreibe, was du mit dem Schieberegler für |
|
Man kann allgemein für eine gebrochen-rationale Funktion Ist n gerade, dann hat die Funktion Ist n ungerade, dann hat die Funktion Die Ordnung der Polstelle |
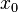 einer gebrochen-rationalen Funktion
einer gebrochen-rationalen Funktion 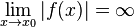 ,
,
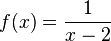
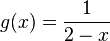
 mit
mit 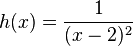
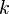 mit
mit 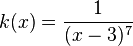
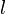 mit
mit 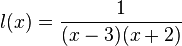
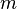 mit
mit 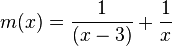
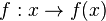 richtig zu!
richtig zu!
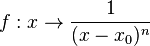 ändern. Beachte den Verlauf des Graphen bei geraden n und bei ungeraden n. Formuliere deine Beobachtung.
ändern. Beachte den Verlauf des Graphen bei geraden n und bei ungeraden n. Formuliere deine Beobachtung.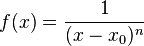 formulieren:
formulieren:
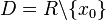 an der Stelle
an der Stelle 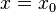 einen Pol ohne Vorzeichenwechsel.
einen Pol ohne Vorzeichenwechsel.

