Rationale Funktionen Polstellen: Unterschied zwischen den Versionen
| Zeile 79: | Zeile 79: | ||
Im folgenden Applet kannst du mit dem Schieberegler die Potenz n des Nenners der Funktion <math>f:x \rightarrow \frac{1}{(x-x_0)^n}</math> ändern. Beachte den Verlauf des Graphen bei geraden n und bei ungeraden n. Formuliere deine Beobachtung.<br> | Im folgenden Applet kannst du mit dem Schieberegler die Potenz n des Nenners der Funktion <math>f:x \rightarrow \frac{1}{(x-x_0)^n}</math> ändern. Beachte den Verlauf des Graphen bei geraden n und bei ungeraden n. Formuliere deine Beobachtung.<br> | ||
| − | |||
| − | |||
<center> | <center> | ||
<ggb_applet width="532" height="492" version="4.2" ggbBase64="UEsDBBQACAAIAFJ2hkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFJ2hkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVhtb9s2EP6c/oqDPrVAbIsS9eLCbtF2KFYg7YqlG4Z92EBLtM1GbxApWy7643ckJVl2k6xLi2JGbJLi8Y733N1DKovnbZ7BjtdSlMXSIVPXAV4kZSqKzdJp1HoSO8+fPVpseLnhq5rBuqxzppYOnXrOcR2OpiTQi0WKWuLE9YOQT4K5506oF/AJ47E7YWuX+YFHOY2ZA9BK8bQo37Gcy4ol/DrZ8pxdlQlTRudWqerpbLbf76e99WlZb2abzWraytQB3Hkhl07XeYrqThbtfSPuuS6Z/fH2yqqfiEIqViTcAe1VI549uljsRZGWe9iLVG2XTkDRjS0Xmy26GXo4mGmhCn2teKLEjktcOhoan1VeOUaMFXr+wvYgG9xxIBU7kfJaozz3Tz8OlLXghepkSWdz1mtb7ATfW7W6ZyzGDqiyzFZMa0Qn4TNg49nGB/hsOoEd024Y2mFkGuJ2T2P9M9eDEIMqpFhlfOmsWSYRJ1Gsa4zRMJbqkHFjtXtw9JFcoidSfEJh30XgLLBme5f6G+KXuh2iI1fIyKqqm3uN2vmjzcFi4Htfb5GOwDMoeK7nwqVuiG08bMLQTrn2GaJqGs821DaBlaF2ObWi1MpQK0P9b4O1d9H7L6B632TzGMj4FptecEcg78sfG7mv8ZMEI5toyvyZ7xcW/fvcPLd4njsPMRjSH+0idefRd3fS98JLEkaXIb3daOTeWiG2JV37Q7BfzHryW3QbArnVsh1TKJ5LvUV/DoHhMAIBFmwYYekFQObYRJoVPSAB0ACHJIZQtxH4mggp+BCDliM+mIoNYvyhkVEWQoDK9NPINawJPoXAB2IKnQLiAIYsEBXPR4kggAAXafPE0yr8EGiIIz8GinvUPBFptvZxIY7RvAc+AV8vJhF4IYQeRJprCNUUFMZ696jVg9CF0ICPbINMY1kGl8Tga4ew+qpSigHgLc+qHicDpSiqRp3Al+Rp31VlNYTRSKdlcvNygLub4UyqsRgeUsej0B5aJyflxSJjK57hfeJa5wLAjmWaXoyFdVko6PPAs882Nau2IpHXXClcJeEj27Erpnj7GqVlb9uYNgf4gjdJJlLBit8xUbQKrRCG81xTRH+eUyxfYyUpyzq9PkjMHmj/5HWJhEniaeT6xKNz84kRzkM3FZEpjeYk7D6aHROm0973p+OD3MNT+XDXVGhN893gGmu57OHf1CId99/Il2WWDlBXpSjUK1appjZ3M9xCrX16UWwybqA1lI+3nORmVbbXFlPf6vpwqHDkWvurzasyK2vAovSCAAW6dmVbI6M3Nki5RsY1Em4fJJEO82TuGQnTrmxrpDDqdmudo6T3kri9GSEN3aDycVaalFk6rQNNIdSVHWGGiuSmc5XYBe+afIXpNqQwCvwk7A3P3mZPzZBbzRy+i5nF7CwPFze8Lnhms63AgDdlI236Dyl8sWgkf8/U9kWR/so3WLjvmeZPhdasqLFoy5EnIseF9nkHMdPh/w13b5+mfFPzTp5l5tJsA2Bm3XHuf/HYqHpdl/mbYvcBc+tsq4tZ789CJrWodAbDCgn9hh+zNBWS4XGQjteh8xK9SDQtIXRK4+oAa9S2rM29GGsbz1V4UdUiQzrFpNVFnfEcb8SgTOoWTc5rkRwz42/XXLdxi03nxRBtHTAoVx+Rgs4CfcQSp+9Ib2BZtWXYm5IuidmB1ydAGW1vy7Q33JnN9O0ecoHcO8G6y1mL5IP6VrLMGoXvNxiZ4vh+Y3fWkRReqvTbU6svzrpzWDpz01mLdgQvIiY+YS6dJsaxzBQS5w2+MkjDBaqretP5WaQpL4bdsgJzyUQEKbDS7uJWkba5rZJhaYXuG74Z5UEXmn8NUnEeIv9/FCLSRYi4Dw9R8ENDRB4SoLaq0ZZW0gG8xiO81Qf94/YJLPGyNIPHLUwAK+rJX4+LJ/ZQPw3suilM9TpHJQ+JIr4I3RFH9944/rJeS64M8qHBfULpfWE2ATlnz1sj4N8XgTGOszGJmZtH9y+JZ/8AUEsHCC4YvGblBQAAQhEAAFBLAQIUABQACAAIAFJ2hkLWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAUnaGQi4YvGblBQAAQhEAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAB8BgAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="532" height="492" version="4.2" ggbBase64="UEsDBBQACAAIAFJ2hkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFJ2hkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVhtb9s2EP6c/oqDPrVAbIsS9eLCbtF2KFYg7YqlG4Z92EBLtM1GbxApWy7643ckJVl2k6xLi2JGbJLi8Y733N1DKovnbZ7BjtdSlMXSIVPXAV4kZSqKzdJp1HoSO8+fPVpseLnhq5rBuqxzppYOnXrOcR2OpiTQi0WKWuLE9YOQT4K5506oF/AJ47E7YWuX+YFHOY2ZA9BK8bQo37Gcy4ol/DrZ8pxdlQlTRudWqerpbLbf76e99WlZb2abzWraytQB3Hkhl07XeYrqThbtfSPuuS6Z/fH2yqqfiEIqViTcAe1VI549uljsRZGWe9iLVG2XTkDRjS0Xmy26GXo4mGmhCn2teKLEjktcOhoan1VeOUaMFXr+wvYgG9xxIBU7kfJaozz3Tz8OlLXghepkSWdz1mtb7ATfW7W6ZyzGDqiyzFZMa0Qn4TNg49nGB/hsOoEd024Y2mFkGuJ2T2P9M9eDEIMqpFhlfOmsWSYRJ1Gsa4zRMJbqkHFjtXtw9JFcoidSfEJh30XgLLBme5f6G+KXuh2iI1fIyKqqm3uN2vmjzcFi4Htfb5GOwDMoeK7nwqVuiG08bMLQTrn2GaJqGs821DaBlaF2ObWi1MpQK0P9b4O1d9H7L6B632TzGMj4FptecEcg78sfG7mv8ZMEI5toyvyZ7xcW/fvcPLd4njsPMRjSH+0idefRd3fS98JLEkaXIb3daOTeWiG2JV37Q7BfzHryW3QbArnVsh1TKJ5LvUV/DoHhMAIBFmwYYekFQObYRJoVPSAB0ACHJIZQtxH4mggp+BCDliM+mIoNYvyhkVEWQoDK9NPINawJPoXAB2IKnQLiAIYsEBXPR4kggAAXafPE0yr8EGiIIz8GinvUPBFptvZxIY7RvAc+AV8vJhF4IYQeRJprCNUUFMZ696jVg9CF0ICPbINMY1kGl8Tga4ew+qpSigHgLc+qHicDpSiqRp3Al+Rp31VlNYTRSKdlcvNygLub4UyqsRgeUsej0B5aJyflxSJjK57hfeJa5wLAjmWaXoyFdVko6PPAs882Nau2IpHXXClcJeEj27Erpnj7GqVlb9uYNgf4gjdJJlLBit8xUbQKrRCG81xTRH+eUyxfYyUpyzq9PkjMHmj/5HWJhEniaeT6xKNz84kRzkM3FZEpjeYk7D6aHROm0973p+OD3MNT+XDXVGhN893gGmu57OHf1CId99/Il2WWDlBXpSjUK1appjZ3M9xCrX16UWwybqA1lI+3nORmVbbXFlPf6vpwqHDkWvurzasyK2vAovSCAAW6dmVbI6M3Nki5RsY1Em4fJJEO82TuGQnTrmxrpDDqdmudo6T3kri9GSEN3aDycVaalFk6rQNNIdSVHWGGiuSmc5XYBe+afIXpNqQwCvwk7A3P3mZPzZBbzRy+i5nF7CwPFze8Lnhms63AgDdlI236Dyl8sWgkf8/U9kWR/so3WLjvmeZPhdasqLFoy5EnIseF9nkHMdPh/w13b5+mfFPzTp5l5tJsA2Bm3XHuf/HYqHpdl/mbYvcBc+tsq4tZ789CJrWodAbDCgn9hh+zNBWS4XGQjteh8xK9SDQtIXRK4+oAa9S2rM29GGsbz1V4UdUiQzrFpNVFnfEcb8SgTOoWTc5rkRwz42/XXLdxi03nxRBtHTAoVx+Rgs4CfcQSp+9Ib2BZtWXYm5IuidmB1ydAGW1vy7Q33JnN9O0ecoHcO8G6y1mL5IP6VrLMGoXvNxiZ4vh+Y3fWkRReqvTbU6svzrpzWDpz01mLdgQvIiY+YS6dJsaxzBQS5w2+MkjDBaqretP5WaQpL4bdsgJzyUQEKbDS7uJWkba5rZJhaYXuG74Z5UEXmn8NUnEeIv9/FCLSRYi4Dw9R8ENDRB4SoLaq0ZZW0gG8xiO81Qf94/YJLPGyNIPHLUwAK+rJX4+LJ/ZQPw3suilM9TpHJQ+JIr4I3RFH9944/rJeS64M8qHBfULpfWE2ATlnz1sj4N8XgTGOszGJmZtH9y+JZ/8AUEsHCC4YvGblBQAAQhEAAFBLAQIUABQACAAIAFJ2hkLWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAUnaGQi4YvGblBQAAQhEAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAB8BgAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
</center> | </center> | ||
| + | Beschreibe, was du mit dem Schieberegler für <math>x_0</math> änderst. | ||
| + | }} | ||
| + | |||
{{Merke|Man kann allgemein für eine gebrochen-rationale Funktion <math> f</math> mit <math> f(x)=\frac{1}{(x-x_0)^n}</math> formulieren: | {{Merke|Man kann allgemein für eine gebrochen-rationale Funktion <math> f</math> mit <math> f(x)=\frac{1}{(x-x_0)^n}</math> formulieren: | ||
| − | Ist n gerade, dann hat die Funktion <math>f:x\rightarrow \frac{1}{(x-x_0)^n}</math> mit <math>D = R \backslash \{x_0\}</math> an der Stelle <math>x = x_0</math> einen '''Pol ohne Vorzeichenwechsel'''. | + | Ist n gerade, dann hat die Funktion <math>f:x\rightarrow \frac{1}{(x-x_0)^n}</math> mit <math>D = R \backslash \{x_0\}</math> an der Stelle <math>x = x_0</math> einen '''Pol ohne Vorzeichenwechsel'''. <math>x_0</math> ist ein Pol gerader Ordnung. |
| − | Ist n ungerade, dann hat die Funktion <math>f:x\rightarrow \frac{1}{(x-x_0)^n}</math> mit <math>D = R\backslash \{x_0\}</math> an der Stelle <math>x = x_0</math> einen '''Pol mit Vorzeichenwechsel'''. | + | Ist n ungerade, dann hat die Funktion <math>f:x\rightarrow \frac{1}{(x-x_0)^n}</math> mit <math>D = R\backslash \{x_0\}</math> an der Stelle <math>x = x_0</math> einen '''Pol mit Vorzeichenwechsel'''. <math>x_0</math> ist ein Pol ungerader Ordnung. |
| − | Die Ordnung der Polstelle <math>x_0</math> ist die Zahl die angibt wie oft <math>x_0</math> Nullstelle des Nenners (des gekürzten Bruches) ist. | + | Die '''Ordnung''' der Polstelle <math>x_0</math> ist die Zahl die angibt wie oft <math>x_0</math> Nullstelle des Nenners (des gekürzten Bruches) ist. |
}} | }} | ||
Aktuelle Version vom 6. April 2013, 13:54 Uhr
Die Funktion 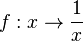 ist für
ist für  nicht definiert. Wie verhält sie sich in der Umgebung von
nicht definiert. Wie verhält sie sich in der Umgebung von  ? Je kleiner
? Je kleiner  betragsmäßig wird, desto größer wird der Betrag von
betragsmäßig wird, desto größer wird der Betrag von  . Zeigt eine Funktion für einen x-Wert ein solches Verhalten, dann ist der x-Wert eine Definitionslücke und man bezeichnet diese Stelle als Polstelle.
. Zeigt eine Funktion für einen x-Wert ein solches Verhalten, dann ist der x-Wert eine Definitionslücke und man bezeichnet diese Stelle als Polstelle.
|
Ist an einer Definitionslücke
dann ist die Definitionslücke |
Beispiele:
1. Die Funktion 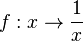 hat für
hat für  einen Pol 1. Ordnung (
einen Pol 1. Ordnung ( ist einfache Nullstelle des Nenners).
ist einfache Nullstelle des Nenners).
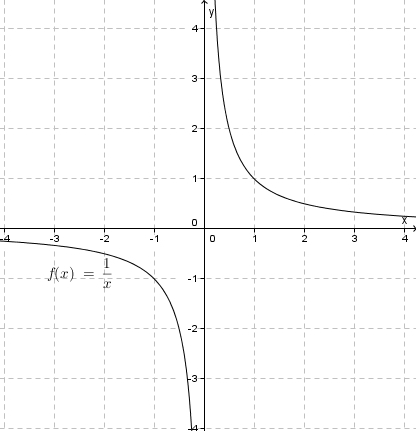
Nähert man sich von links an, also 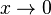 mit
mit 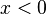 , dann streben die Funktionswerte nach
, dann streben die Funktionswerte nach 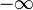 ; nähert man sich von rechts an, also
; nähert man sich von rechts an, also 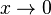 mit
mit 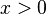 , dann streben die Funktionswerte nach
, dann streben die Funktionswerte nach 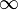 .
.  hat an
hat an  eine Polstelle mit Vorzeichenwechsel. Die Gerade
eine Polstelle mit Vorzeichenwechsel. Die Gerade  ist senkrechte Asymptote des Graphen von
ist senkrechte Asymptote des Graphen von  .
.
2. Die Funktion 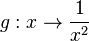 hat für
hat für  einen Pol 2. Ordnung (
einen Pol 2. Ordnung ( ist zweifache Nullstelle des Nenners).
ist zweifache Nullstelle des Nenners).
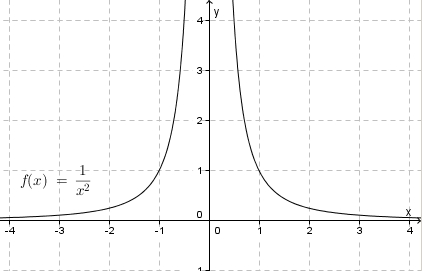
Nähert man sich von links oder von rechts an, also 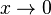 mit
mit 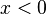 oder
oder 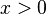 , dann streben die Funktionswerte in beiden Fällen nach
, dann streben die Funktionswerte in beiden Fällen nach 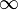 .
. 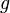 hat an
hat an  eine Polstelle ohne Vorzeichenwechsel. Die Gerade
eine Polstelle ohne Vorzeichenwechsel. Die Gerade  ist senkrechte Asymptote des Graphen von
ist senkrechte Asymptote des Graphen von  .
.
|
Ermittle bei den gegebenen Funktionen jeweils die Polstelle(n) der Funktion und beschreibe das Vorzeichenverhalten der Funktion bei Annäherung an die Polstelle(n). a) b) c) d) e) f) |
a) x = 2; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<2): 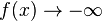 ; Annäherung von rechts (x>2):
; Annäherung von rechts (x>2): 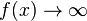
b) x = 2; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<2): 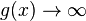 ; Annäherung von rechts (x>2):
; Annäherung von rechts (x>2): 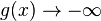
c) x = 2; Pol 2. Ordnung; Pol ohne Vorzeichenwechsel; Annäherung von links (x<2): 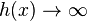 ; Annäherung von rechts (x>2):
; Annäherung von rechts (x>2): 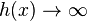
d) x = 3; Pol 7. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<3): 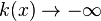 ; Annäherung von rechts (x>3):
; Annäherung von rechts (x>3): 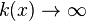
e) x = -2; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<-2): 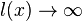 ; Annäherung von rechts (x>-2):
; Annäherung von rechts (x>-2): 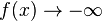
- x = 3; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<3):
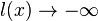 ; Annäherung von rechts (x>3):
; Annäherung von rechts (x>3): 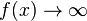
e) x = 0; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<-2): 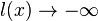 ; Annäherung von rechts (x>-2):
; Annäherung von rechts (x>-2): 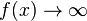
- x = 3; Pol 1. Ordnung; Pol mit Vorzeichenwechsel; Annäherung von links (x<3):
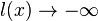 ; Annäherung von rechts (x>3):
; Annäherung von rechts (x>3): 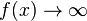
|
Ordne die Polstellen und die angegebenen Funktionen |
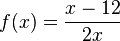 |

|
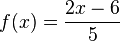 |
keine Polstelle |
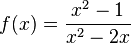 |
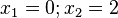
|
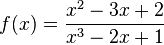 |
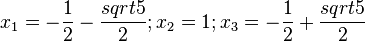
|
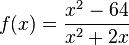 |
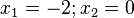
|
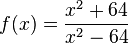 |
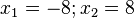
|
|
Im folgenden Applet kannst du mit dem Schieberegler die Potenz n des Nenners der Funktion
Beschreibe, was du mit dem Schieberegler für |
|
Man kann allgemein für eine gebrochen-rationale Funktion Ist n gerade, dann hat die Funktion Ist n ungerade, dann hat die Funktion Die Ordnung der Polstelle |
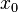 einer gebrochen-rationalen Funktion
einer gebrochen-rationalen Funktion 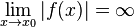 ,
,
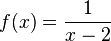
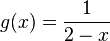
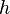 mit
mit 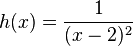
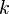 mit
mit 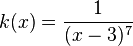
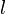 mit
mit 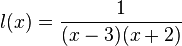
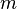 mit
mit 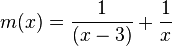
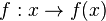 richtig zu!
richtig zu!
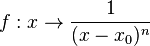 ändern. Beachte den Verlauf des Graphen bei geraden n und bei ungeraden n. Formuliere deine Beobachtung.
ändern. Beachte den Verlauf des Graphen bei geraden n und bei ungeraden n. Formuliere deine Beobachtung.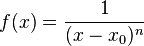 formulieren:
formulieren:
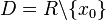 an der Stelle
an der Stelle 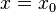 einen Pol ohne Vorzeichenwechsel.
einen Pol ohne Vorzeichenwechsel. 
