Rationale Funktionen hebbare Definitionslücken: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
Die neue Funktion <math>\tilde f:x\rightarrow \frac{1}{x+2}</math> ist für <math> x = 1 </math> mit dem Funktiionswert <math>\tilde f(1) = \frac{1}{3}</math> definiert. Man kann also die Funktion <math> f</math> in die hebbare Definitionslücke fortsetzen. Nimmt man den Funktionswert von <math>\tilde f(1)=\frac{1}{3}</math>, dann hat man die Funktion sogar stetig fortgesetzt. | Die neue Funktion <math>\tilde f:x\rightarrow \frac{1}{x+2}</math> ist für <math> x = 1 </math> mit dem Funktiionswert <math>\tilde f(1) = \frac{1}{3}</math> definiert. Man kann also die Funktion <math> f</math> in die hebbare Definitionslücke fortsetzen. Nimmt man den Funktionswert von <math>\tilde f(1)=\frac{1}{3}</math>, dann hat man die Funktion sogar stetig fortgesetzt. | ||
| + | |||
| + | {{Aufgabe|1= | ||
| + | Im folgenden Applet wird die Funktion <math>f:x \rightarrow f(x) = \frac{(x+3)(x-2)^2}{(x-2)^n} </math> dargestellt . <br> | ||
| + | Variiere mit dem Schieberegler den Wert des Exponenten der Nennerpotenz. <br> | ||
| + | |||
| + | Beobachte die Veränderungen für <math>x=2</math> beim Variieren von n. Formuliere deine Beobachtung. | ||
| + | <center> | ||
| + | <ggb_applet width="532" height="492" version="4.2" ggbBase64="UEsDBBQACAAIAD15hkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAD15hkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVdtb9s2EP6c/oqDPiVbbIsi9eLCbtFuKFYg7YqlG4Z9GEBLtM1GlgSRsuWiP35HUpKVNAm6tqhhm6R4vIf33AupxfN2l8Ne1EqWxdIjU98DUaRlJovN0mv0epJ4z589WWxEuRGrmsO6rHdcLz02DbzTOhxNSWgWywy1JKlPw0hMwnngT1gQigkXiT/ha5/TMGCCJdwDaJV8WpRv+U6oiqfiOt2KHb8qU66tzq3W1dPZ7HA4THv0aVlvZpvNatqqzAPceaGWXtd5iupuLTpQKx74Ppn9/ebKqZ/IQmlepMIDY1Ujnz05WxxkkZUHOMhMb5deyNCMrZCbLZoZBTiYGaEKba1EquVeKFw6Glqb9a7yrBgvzPyZ60E+mONBJvcyE7Vhec4SMvoilWUtRaE7WdJhznpti70UB6fW9Cxi4oEuy3zFjUY0Ej4BNoFrKMAn2wndmHXDyA1j2xC/e5qYv7kZROhUqeQqF0tvzXOFPMliXaOPhrHSx1xY1O7ByUZySXFefkRh6iNxjli7vUvzi/DH/I7RkSlkhKrr5lFQN3/CHBBDGnw5IhuRZ1kI/MCHS9MQ1wTYRJGb8t0zZNU2gWuYa0Inw9xy5kSZk2FOhtFvo7U3Mfg/pAbfhHlyZHIPZhA+4MjH4sd57kvsJOEIE6Hs1/4+Q6SPmXkX8W7sfA1gxH60icyfx9/dSMzPS+qzy4jdDxr792aIa0nX/hDuF7O++C26DYHaGtmuUmixU2aLdA6hrWEEQkzYKMbUC4HMsYlNVQyAhMBCHJIEItPGQE0hZEAhASNHKNiMDRP8Y7FVFkGIyszT2LdVEyiDkAKxic4AeQBbLJCVgKJEGEKIiww8CYwKGgGLcEQTYLhHUydiU60pLsQxwgdACVCzmMQQRBAFEJtaQ5gpQVFido9aA4h8iCz5WG2w0rgqg0sSoMYgzL6qVHIgeCvyqufJUimLqtG36Et3Wd/VZTW40UpnZXrzcqC7mxFc6bEYHlKno9AdWrdOyrNFzlcix/vEtYkFgD3PTXmxCOuy0NDHQeCebWpebWWqroXWuErBB77nV1yL9hVKqx7bQtsDfCGaNJeZ5MVfGChGhVEIw3luSkR/njNMX4uSlmWdXR8VRg+0/4i6xIJJkmnsUxKwuftgph+7qZhMWTwnUfcx1THlJuwpndLRJ0jQB8eH5yy22A+28Vaonv9NLbNx/7V6WebZwHVVykL/wivd1PZyhnuojVEvik0uLLe25uM1J71Zle21I5U6Xe+PFY58h7/a/FLmZQ2YlUEYokDXrlxrZczGBinfyvhWwu+9JLNhnswDK2HblWutFLrdba0zlPRWEr+HkcrWG1Q+DksbM0uv9aAppL5yIwxRmd50phK34G2zW2G8DTGMAr9Kd8Vz19nbMORemON3gVnM7gTi4kbUhchduBXo8KZslIv/IYbPFo0S77jeviiyP8QGM/cdNwVUI5oTtYguH0Uqd7jQPe8o5sb9f+Lu3dNMbGrRyfPc3pqdA+ysPw7+zx5bVa/qcve62L/H2Lqz1cWst2eh0lpWJoJhhRX9RpyiNJOK43mQjdeh8QqtSE1dQuq04dUD3uhtWduLMSY3HqzwoqpljvUUg9ZkdS52eCUGbUO3aHailungssLetnGDTWcD631t3AXl6gNWoDtuPjGJ0w8EN/C82nLsTUkXwvwo6ls0WW1vyqwD7uRUbi73sJOu9O54a2+ZfKXKvNH4doNuKU5vN25jXYnCK5V5d2ptycDOER/Fc9Nby3ZELvIlP2Ik3Q6LU5JprJs3+MagbCXQXc7bzm8yy0Qx7JYXGEnWH1gBKxfmlRAuQ4aFFRpva80oBjq3GAe1VY1YRklH8BqPh9YcIuftBSzh/LyFn4FewE+AvQkEF/+eBxcXMDsNiwt3iNx29ropbLB4J8Vf41m8eD/gW/9R3/6+XiuhjTsmofNGFDzm+nsdQB9zwJjG2Tg97KHWve0++w9QSwcITiMD1swFAACdDwAAUEsBAhQAFAAIAAgAPXmGQtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAA9eYZCTiMD1swFAACdDwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAGMGAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | </center> | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1= | ||
| + | Für n = 4 und n = 3 ist <math>x=2</math> nicht hebbare Definitionslücke. Der Graph hat an der Stelle <math>x=2</math> eine Polstelle ohne bzw. mit Vorzeichenwechsel. | ||
| + | |||
| + | Für n = 2 ist die Definitionslücke <math>x=2</math> hebbar. Am Graph sieht man | ||
| + | }} | ||
{{Arbeiten|NUMMER=1| | {{Arbeiten|NUMMER=1| | ||
Version vom 6. April 2013, 14:19 Uhr
Die Funktion Fehler beim Parsen(Unbekannte Funktion „\fra“): f:x\rightarrow \fra{x-1}{x^2+x-2}
ist an den Nullstellen des Nenners, also für
nicht erklärt. Vereinfacht man den Funktionsterm
so ist der gekürzte Term
für
erklärt mit dem Wert
. Man sagt, dass
eine hebbare Definitionslücke ist.
|
Ist |
Die neue Funktion 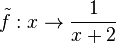 ist für
ist für 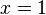 mit dem Funktiionswert
mit dem Funktiionswert 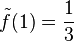 definiert. Man kann also die Funktion
definiert. Man kann also die Funktion  in die hebbare Definitionslücke fortsetzen. Nimmt man den Funktionswert von
in die hebbare Definitionslücke fortsetzen. Nimmt man den Funktionswert von 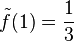 , dann hat man die Funktion sogar stetig fortgesetzt.
, dann hat man die Funktion sogar stetig fortgesetzt.
|
Im folgenden Applet wird die Funktion Beobachte die Veränderungen für
|
Für n = 4 und n = 3 ist 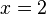 nicht hebbare Definitionslücke. Der Graph hat an der Stelle
nicht hebbare Definitionslücke. Der Graph hat an der Stelle 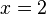 eine Polstelle ohne bzw. mit Vorzeichenwechsel.
eine Polstelle ohne bzw. mit Vorzeichenwechsel.
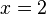 hebbar. Am Graph sieht man
hebbar. Am Graph sieht man|
Gib jeweils für die Funktion a) b) c) d) e) f) g) |
a) 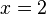 ist eine Definitionslücke; wegen
ist eine Definitionslücke; wegen 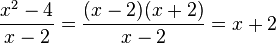 ist
ist 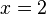 hebbare Definitionslücke mit
hebbare Definitionslücke mit 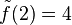 .
.
b) 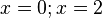 sind Definitionslücken; wegen
sind Definitionslücken; wegen 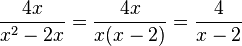 ist
ist  hebbare Definitionslücke mit
hebbare Definitionslücke mit 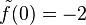 .
.
c) 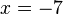 ist Definitionslücke; da man den Bruchterm nicht kürzen kann, ist
ist Definitionslücke; da man den Bruchterm nicht kürzen kann, ist 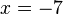 keine hebbare Definitionslücke.
keine hebbare Definitionslücke.
d) 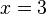 ist Definitionslücke; da man den Bruchterm nicht kürzen kann, ist
ist Definitionslücke; da man den Bruchterm nicht kürzen kann, ist 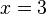 keine hebbare Definitionslücke.
keine hebbare Definitionslücke.
e) 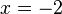 ist Definitinoslücke; wegen
ist Definitinoslücke; wegen 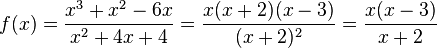 ist
ist 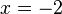 weiterhin Definitionslücke und nicht hebbar.
weiterhin Definitionslücke und nicht hebbar.
f) 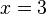 ist Definitionslücke; wegen
ist Definitionslücke; wegen 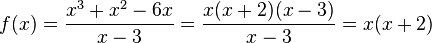 ist
ist 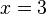 eine hebbare Definitionslücke mit
eine hebbare Definitionslücke mit 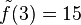 .
.
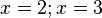 sind Definitionslücken; wegen
sind Definitionslücken; wegen 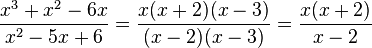 eine hebbare Definitionslücke mit
eine hebbare Definitionslücke mit 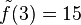 .
.|
Ordne die hebbare bzw. nicht hebbare Definitionslücke und die angegebene Funktion |
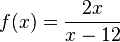 |
x=12 ist nicht hebbare Definitionslücke. |
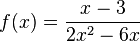 |
x=3 ist hebbare Definitionslücke. |
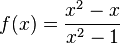 |
x=1 ist hebbare Definitionslücke. |
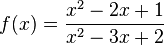 |
x=2 ist nicht hebbare Definitionslücke. |
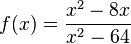 |
x=8 ist hebbare Definitionslücke. |
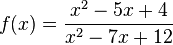 |
x=3 ist nicht hebbare Definitionslücke. |
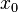 eine Nullstelle des Zählers und des Nenners der gebrochen-rationalen Funktion
eine Nullstelle des Zählers und des Nenners der gebrochen-rationalen Funktion 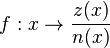 und existiert der Grenzwert
und existiert der Grenzwert 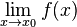 , so nennt man
, so nennt man 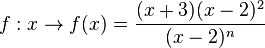 dargestellt .
dargestellt . 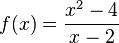
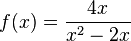
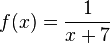
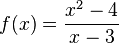
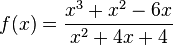
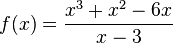
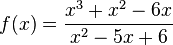
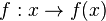 richtig zu!
richtig zu!

