Didaktischer Kommentar

Zurück zur Startseite

---

Der Lernpfad "Funktionen - Einstieg" kann zum Einstieg in das Thema Funktionen in der 5. Klasse AHS (9. Schulstufe) eingesetzt werden. Anhand konkreter Aufgabenstellungen soll mit Hilfe des Einsatzes elektronischer Medien Vorwissen aus der Unterstufe aktiviert und vertieft (verschiedene Darstellungsformen für Funktionen wie Formel, Wertetabelle, Graph) sowie neue Kenntnisse zum Funktionsbegriff (Präzisierung der Funktionsdefinition, Bezeichnungen wie Definitionsmenge, Zielmenge, Argument, Funktionswert,…) erarbeitet und an komplexeren Aufgabenstellungen angewendet werden.

Kurzübersicht

Schulstufe 5. Schulstufe in Österreich bzw. 10. Jahrgangsstufe in Deutschland Unterrichtsfächer Mathematik Dauer Dauer ca. 8 UE Technische Voraussetzungen Internet und Java, GeoGebra einschließlich Tabellen und CAS, YouTube für Videos, Flash Medien Java-Applets, GeoGebra einschließlich Tabellen und CAS, Bilder, interaktive Tests Lernziele Kenntnis und Handhabung von Wertetabelle, Graph und Funktionsterm als Darstellungsmöglichkeiten von Funktionen Übersetzen von einer Realsituation in ein mathematisches Modell Verstehen einer exakten Definition der Funktion und des Funktionsgraphen Wechseln zwischen den Darstellungsformen Graph, Tabelle und Formel Funktionen als mathematische Objekte erkennen Kenntnis von Eigenschaften von Funktionen Kompetenzen Operieren, Interpretieren, Kommunizieren, Argumentieren, Dokumentieren, Transferieren Methodik Gruppenarbeit, Lernen an Stationen Autoren Irma Bierbaumer, Franz Embacher, Helmut Heugl (2006), überarbeitet von Karl Haberl (2012) Zur Nutzung dieses Lernpfades Einsatz des Lernpfades als Lernsequenz Der verbindende Text soll als Leitfaden für das selbstgesteuerte Lernen dienen. Einsatz im Rahmen einer Lernspirale Der modulartige Aufbau erlaubt einen Einsatz nach individuellen methodischen Vorstellungen (nach eigenem "Drehbuch"). Die in diesem Kapitel angesprochenen Grundfähigkeiten und Grundfertigleiten sollten aber auf jeden Fall vermittelt werden. Dabei kann die Übersicht eine Art Leitlinie hierzu sein. Dabei sind Pflichtaufgaben, Wahlpflichtaufgaben oder Bonusaufgaben zu bearbeiten. Gruppenarbeit Grundsätzlich kann der Lernpfad auch in Gruppenarbeit bearbeitet werden. Dabei können einzelne Aufgaben für leine Gruppe ausgewählt werden, die dann den anderen Gruppen vorgestellt werden müssen. Gerade "Eigenschaften von Funktionen" bietet sich für Expertengruppen an. Lernen an Stationen Man kann den Lernpfad auch als "Lernen an Stationen" auffassen, und den SchülerInnen einen Lernplan mitgeben, auf dem sie notieren, was schon bearbeitet wurde. Das Arbeitsblatt für SchülerInnen kann hier heruntergeladen und dann ausgedruckt werden. Dabei sind Pflichtaufgaben, Wahlpflichtaufgaben oder Bonusaufgaben zu bearbeiten. Didaktische Grundlagen Zur fundamentalen Idee der "Funktion" Allgemeinbegriffe erwirbt man in der Regel durch die Erfahrung und Begegnung mit prototypischen Repräsentanten (den Begriff "Tisch" verinnerlicht man nicht, indem man eine exakte Definition gibt, sondern weil man verschiedene Prototypen des Tisches erlebt). So verinnerlichen Lernende die fundamentale Idee der Funktion auch nicht durch eine "saubere" Definition am Beginn des Lernprozesses, sondern indem er verschiedene Prototypen dieses Begriffes möglichst anhand von Beispielen aus seiner Erfahrungswelt erlebt [Dörfler, 1991]. Im Laufe des "Funktionenlernens" erleben Lernende verschieden Prototypen des Funktionsbegriffes: 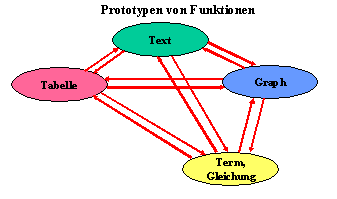"Funktionenlernen" besteht im Wesentlichen darin, einen Prototypen zu finden, Beziehungen zwischen Prototypen herzustellen oder bestimmte Prototypen für das Problemlösen zu nutzen. Funktionenlernen an "Prototypen" in diesem Lernpfad Text <-> Tabelle <-> Formel (=Funktionsgleichung) <-> Tabelle <-> Graf Handybeispiel (1): Aus einem Text eine Tabelle, eine Gleichung finden. Handybeispiel (2): Mit einem geeigneten elektronischen Werkzeug eine Tabelle erstellen. Handybeispiel (3): Die Tabelle zum Problemlösen nutzen. Schachtelbeispiel (1): Aus einem Text, einer Skizze, einer Flashanimation eine Formel (Funktionsgleichung) finden. Schachtelbeispiel (2): Aus einer Formel eine Tabelle mit variabler Schrittweite erstellen. Handybeispiel (4) und Schachtelbeispiel (3): Aus dem Text bzw. der Funktionsgleichung Eigenschaften der jeweiligen Funktionen ableiten können. Schachtelbeispiel (5), Handybeispiel (4) und (5): Aus Gleichungen und Tabellen Graphen mit Hilfe geeigneter elektronischer Werkzeuge ermitteln können. Zum genetischen Konzept Anschluss an das Vorverständnis der Adressaten. Probleme, wie z.B. Handytarife, kommen aus der Erfahrungswelt der Schülerinnen und Schüler. Zulässigkeit einer informellen Einführung. Eine "saubere" Definition des Funktionsbegriffes erfolgt erst, wenn die Schülerinnen und Schüler schon längst mit verschiedenen Funktionsprototypen Bekanntschaft gemacht haben. Hinführen zu strengeren Überlegungen; Erweiterung des Gesichtskreises, Standpunktsverlagerung. Die Aufgabensequenz soll den Schülerinnen und Schülern die Notwendigkeit einer exakteren Fassung des Funktionsbegriffes klar machen (Definitions- und Zielmenge, usw.) Durchgehende Motivation, Kontinuität. Die Schülerinnen und Schüler sollten auch das Gemeinsame in dieser Aufgabensequenz erkennen und den Zusammenhang der einzelnen Phasen verstehen. Drei Phasen des Mathematiklernens Die experimentelle, heuristische Phase: Durch experimentieren mit verschiedenen Funktionsprototypen (Tabelle, Graf, usw.) erfahren die Schülerinnen und Schüler die wichtigsten Kennzeichen funktionaler Abhängigkeiten. Die exaktifizierende Phase: Sie besteht in diesem Lernpfad in der Definition der Funktion und des Funktionsgraphen. Beweise im engeren Sinn findet man erst in späteren Teilen des Kapitels "Funktion". Die Anwendungsphase: Anwendungen begleiten den ganzen Lernprozess. Aus den Anwendungen wird auch der Funktionsbegriff erarbeitet. Im letzten Teil werden dann noch Aufgaben zur Festigung des Gelernten und eventuell zur Selbstevaluation und als Übungsaufgaben angeboten. Grundvorstellungen - Grundfähigkeiten Grundvorstellungen zu Funktionen Grundvorstellung 1: Einen naiven Funktionsbegriff verinnerlichen: "Abhängigkeiten zwischen Größen" Grundvorstellung 2: Beziehungen zwischen verschiedenen "Prototypen" des Funktionsbegriffes herstellen und nutzen können: Text <-> Tabelle Text <-> Term Term <-> Tabelle Tabelle <-> Graph Term <-> Graph Grundvorstellung 3: Einen exakteren Funktionsbegriff verinnerlichen. Grundfähigkeiten zu Funktionen Grundfähigkeit 1: Mit Informationen aus einem Text eine Tabelle erstellen können Grundfähigkeit 2: Tabelle zum Interpretieren, zum Problemlösen nutzen können Grundfähigkeit 3: Aus einem Text, einer Tabelle einen Funktionsterm entwickeln können Grundfähigkeit 4: Aus einem Text, einer Tabelle, einem Term einen sinnvollen Definitionsbereich ableiten können Grundfähigkeit 5: Aus einer Tabelle, einem Funktionsterm einen Graphen zeichnen können Grundfähigkeit 6: Graphen interpretieren können Grundfähigkeit 7: Für alle diese Grundfähigkeiten technologische Hilfsmittel nutzen können Genderaspekte Der Lernpfad ist so ausgelegt, dass er Mädchen und Jungen gleichermaßen anspricht. Die Applets sind für beide Geschlechter gleich gut geeignet. Es handelt sich wesentlich um mathematische Themen, die Beispiele sind für beide Geschlechter anschaulich und aus ihrer Erfahrungswelt gegriffen. Es müssen daher keine Alternativen für geschlechterspezifische Aufgaben angegeben werden. Die Aufgaben bei den Eigenschaften von Funktionen sind rein mathematisch orientiert und damit geschlechtsunabhängig. Der Lernpfad ist gleichermaßen für Jungen wir Mädchen geeignet. Kompetenzen Auf der Seite Kompetenzen sind die geförderten Kompetenzen ausführlich beschreiben. Insgesamt werden alle Handlungskompetenzen Modellieren - Transferieren - Operieren - Interpretieren - Dokumentieren - Argumentieren - Kommunizieren genutzt, gefordert und gefördert. Literatur Dörfler, Willi. (1991): "Der Computer als kognitives Werkzeug und kognitives Medium" in Computer - Mensch - Mathematik. Verlag Hölder-Pichler-Tempsky, Wien, 1991, S. 51. ISBN3-209-01452-3. Zurück zur Startseite